Урок 13. Подобие разносторонних треугольников

ВИДЕОУРОК

Отношение отрезков.

Отношение отрезков  АВ  и  СD – отношение их длин то есть

– отношение отрезков  АВ  и  СD.

ПРИМЕР:

Отрезки длиной  2 см  и  3 см  пропорциональны отрезкам длиной  4 см  и  6 см, так как

Пропорциональными могут быть не только пары отрезков, но и большее их число.

ПРИМЕР:

Отрезки  

а, b, с, d  

пропорциональны отрезкам  

а₁, b₁, с₁, d₁, 

если

Сходственные стороны – стороны треугольников, у которых противоположные им углы соответственно равны.

Подобные треугольники – треугольники, углы которых соответственно равны, а стороны одного треугольника пропорциональны сходственным сторонам другого.

ПРИМЕР:

Если  

∠ А = ∠ А₁, 
∠ В = ∠ В₁, 
∠ С = ∠ С₁,

то  ∆ АВС ~ ∆ А₁В₁С₁
Подобие треугольников   АВС  и  А₁В₁С₁  коротко записывают так:

∆ АВС  ~ ∆ А₁В₁С₁.

Знак  ~  заменяют словом подобный.

Две фигуры подобны, если каждой точке одной фигуры можно сопоставить точку другой фигуры так, что для любых двух точек  А  и  В  одной фигуры и сопоставимых им точек  А₁  и  В₁  другой фигуры выполняется условие

где  k – одно и то же положительное число для всех точек.

Число  k – коэффициент подобия фигур.

Примерами подобных фигур произвольной формы являются две географические карты одной и той же местности, выполненные в разных масштабах; фотографии одного и того же предмета, сделанные при разных увеличениях.

Коэффициент подобия – число, равное отношению сходственных сторон треугольника.

Если коэффициент подобия известен, то записывают:

Для подобных треугольников имеет значение порядок записи вершин. Чтобы составить отношение  сторон подобных треугольников необходимо:

– определить равные углы треугольников;

– выяснить, какие стороны будут сходственными;

– записать соответствующие отношения.

Признаки подобия разносторонних треугольников.

– если три стороны одного треугольника пропорциональны трём сторонам другого, то такие треугольники подобны;

где  k – коэффициент подобия.

– если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны;

– если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а заключённые между ними углы равны, то такие треугольники подобны;

Средняя линия отсекает треугольник который подобен данному, а его площадь равна одной четвёртой площади исходного треугольника.
Отношение периметров подобных треугольников равно отношению сходственных сторон (коэффициенту подобия):

Отношение сходственных линейных элементов (медиан, биссектрис, высот и так далее) подобных треугольников тоже равно коэффициенту подобия. Прямая, которая параллельна стороне треугольника и пересекает две другие его стороны, отсекает от него подобный ему треугольник.

Отношение площади подобных треугольников равно квадрату отношения соответствующих сторон (квадрату коэффициента подобности).

Правильные  n – угольники подобны. Отношение их  периметров, радиусов вписанных и описанных окружностей равны отношению их сторон, а отношение их площадей – отношению квадратов сторон. 

Площади подобных фигур пропорциональны квадратам сходственных линейных элементов (сторон, высот, диагоналей).

ЗАДАЧА:

∆ АВС ~ ∆ А₁В₁С₁.

Найдите неизвестные стороны треугольника, если

АВ = 18 см, АС = 16,4 см,

А₁В₁ = 9 см, 

В₁С₁ = 7 см.

РЕШЕНИЕ:

Поэтому

Откуда

BC = 2В₁С₁,

BC = 2 ∙ 7 = 14 (см).

A₁С₁ = AC : 2,

A₁С₁ = 16,4 : 2 = 8,2 (см).

ОТВЕТ:  14 см, 8,2 см

ЗАДАЧА:

На стороне  АС  треугольника  АВС  обозначена точка  D  так, что 

∠ АВD = ∠ АСВ.

Найдите отрезок  АD, если

АВ = 6 см, АС = 18 см.

РЕШЕНИЕ:

Начертим чертёж.

∆ ABC ~ ∆ AВD 
(угол А – общий, ∠ АВD = ∠ С). Тогда:

AD = 2 (см).

ЗАДАЧА:

На стороне  ВС  треугольника  АВС  обозначена точка  К  так, что

∠ САК = ∠ АВС,

ВК = 12 см, КС = 4 см.

 Найдите сторону  АС.

РЕШЕНИЕ:

Начертим чертёж.

∆ АВС ~ ∆ КАС 
(по двум углам).

АС² = ВС ∙ КС =

= (12 + 4) ∙ 4 = 64,

АС = 8 (см).

ЗАДАЧА:

Диагонали трапеции  ABCD  (AD ∥ BC)  пересекаются в точке  О.

ВО : ОD = 2 : 7,

ВС = 18 см.

Найдите основание  AD  трапеции.

РЕШЕНИЕ:

Начертим чертёж.

∆ ВОС ~ ∆ DАО

АD = 63 см.

ЗАДАЧА:

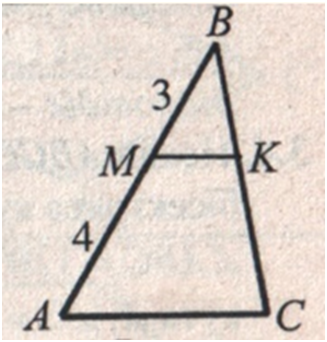
Прямая, параллельная стороне  АС  треугольника  АВС, пересекает сторону  АВ  у точке  М, а сторону  ВС – в точке  К. Найдите площадь треугольника  АВС, если

ВМ = 3 см, АМ = 4 см,

а площадь четырёхугольника  АМКC  равна  80 см².

РЕШЕНИЕ:

Начертим чертёж.

S_ABC = x,

x = 98 (см²).

ЗАДАЧА:

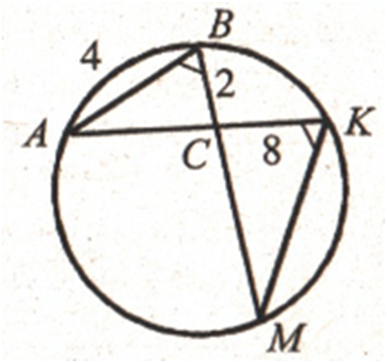
В окружности проведены хорды  АК  и  ВМ, которые пересекаются в точке  С. Найдите отрезок  КМ, если

АВ = 4 см,

ВС = 2 см,

КС = 8 см.

РЕШЕНИЕ:

Начертим чертёж.

∠ В =∠ К = ¹/₂ ∪ АМ,

∠ КСМ = ∠ ВСА – как вертикальные.

∆ АВС ~ ∆ МКС.

КМ = 16 см.

ЗАДАЧА:

В трапеции  ABCD  известно, что  BC ∥ AD, K – точка пересечения диагоналей,

АK : KС = 9 : 4,

DK – BK = 15 см.

Найдите диагональ  BD.

РЕШЕНИЕ:

ABCD – трапеция,

BC ∥ AD, АK : KС = 9 : 4,

DK – BK = 15 см.

BK = DK – 15.

∆ AКD ~ ∆ ВКС

5DK = 135, DK = 27 (см).

BK = DK – 15 = 27 – 15 = 12 (см).

BD = BK + КD = 12 + 27 = 39 (см).

ОТВЕТ:  39 см

ЗАДАЧА:

Продолжение боковых сторон  АВ  и  СD  трапеции  АВСD  пересекаются в точке  K. Большее основание  АD трапеции равно     18 см, АК = 24 см, АВ = 16 см. Найдите меньшее основание трапеции.

РЕШЕНИЕ:

Начертим чертёж.

∆ ВКС ~ ∆ AКD

ЗАДАЧА:

Через точку  О,  точку пересечения диагоналей трапеции  ABCD,  проведена прямая, которая пересекает основание  AD  и  BC  в точках  Е  и  F  соответственно. Найдите отрезок  ВF, если

DЕ = 15 см, 

ОА : ОС = 3 : 2.

РЕШЕНИЕ:

Начертим чертёж.

∆ FCO ~ ∆ EAO

∆ EOD ~ ∆ FOB

ЗАДАЧА:

В треугольник  АВС  вписан ромб  АМКР  так, как показано на рисунке.

Найдите сторону ромба, если

АВ = 18 см, АС = 12 см.

РЕШЕНИЕ:

Пусть сторона ромба равна  х.

Тогда  РС = 12 – х.

∆ АВС ~ ∆ РКС

18(12 – х) = 12х,

х = 7,2 (см).

ЗАДАЧА:

Продолжения боковых сторон  АВ  и  СD  трапеции  АВСD  пересекаются в точке  F,

АВ : BF = 3 : 7,

АD – большее основание трапеции. Разность оснований трапеции равна  6 см. Найдите основание  АD.

РЕШЕНИЕ:

Начертим чертёж.

∆ ВFС ~ ∆ AFD

BC = 7x,

АD = 10x,

10x – 7x = 6,

3x = 6, x =2.

АD = 20 см

ЗАДАЧА:

Основания равнобедренной трапеции равны  20 см  и  28 см, а боковая сторона – 5 см. Найдите площадь трапеции, подобной данной, высота которой равна  12 см.

РЕШЕНИЕ:

Пусть  АВСD – данная равнобедренная трапеция, у которой

ВС = 20 см,

АD = 28 см,

АВ = 5 см.

Проведем 

BN ⊥ AD, CK ⊥ AD,

∆ ABN = ∆ DCK

(как прямоугольные, у которых равны гипотенузы и катеты).

NВСК – прямоугольник.

АN = KD = (28 – 20) : 2 = 4 (см).

Из прямоугольного треугольника  АВN  по теореме Піфагора

AB² = BN² + AN².

ОТВЕТ:  1152 см²

ЗАДАЧА:

Непараллельные стороны трапеции продолжены до взаимного пересечения и через полученную точку проведена прямая, параллельная основаниям трапеции. Найти отрезок  АВ, если основания трапеции равны  a  и  b (a ˃ b) 

DE = a, MN = b.

РЕШЕНИЕ:

∆ DME ~ ∆ AMC;

∆ DNE ~ ∆ CNB;

∆ MNE ~ ∆ ACE;

Откуда

поэтому

и тогда

Поэтому,

Задания к уроку 13

• Задание 1
• Задание 2
• Задание 3

Другие уроки:

• Урок 1. Единицы измерения площади
• Урок 2. Площадь прямоугольника
• Урок 3. Площадь квадрата
• Урок 4. Площадь треугольника
• Урок 5. Площадь прямоугольного треугольника
• Урок 6. Площадь равнобедренного треугольника
• Урок 7. Площадь параллелограмма
• Урок 8. Площадь ромба
• Урок 9. Площадь трапеции
• Урок 10. Площадь равнобедренной трапеции
• Урок 11. Площадь прямругольной трапеции
• Урок 12. Площадь круга и его частей
• Урок 14. Подобие равнобедренных треугольников
• Урок 15. Подобие прямоугольных треугольников
• Урок 16. Площадь многоугольника