Урок 5. Площадь прямоугольного треугольника

ВИДЕОУРОК

Площадь прямоугольного треугольника равна половине произведения его катетов.

где  a  и  b – катеты прямоугольного треугольника.

ЗАДАЧА:

Найдите площадь треугольника  АВС, изображённого на рисунку.

РЕШЕНИЕ:

∠ BDC = 180° – 135° = 45°,

∠ DBC = 45°, DC = ВC = √͞͞͞͞͞2 см,

BD = √͞͞͞͞͞2 BC = 2 см, AD = BD = 2 см,

S = ¹/₂ (AD + DC) BC =

= ¹/₂ (2 + √͞͞͞͞͞2)√͞͞͞͞͞2 = (√͞͞͞͞͞2 + 1) (см²).

ЗАДАЧА:

В прямоугольном треугольнике  АВС  катеты равны  6 см  и  8 см. Найдите высоту  ВК, опущенную на гипотенузу  АС.

РЕШЕНИЕ:

Пусть катет 

АВ = 6 см, а  ВС = 8 см.

Тогда по теореме Пифагора найдём гипотенузу:

Площадь прямоугольного треугольника равна половине произведения катетов, то есть:

S = ¹/₂ AB ∙ DC = 24 см².

Высоту  ВК  найдём по формуле:

ЗАДАЧА:

Катеты прямоугольного треугольника равны  8 см  и  15 см. Найдите расстояние от вершины большего острого угла треугольника до центра вписанной окружности.

РЕШЕНИЕ:

Пусть  АВС (∠ С = 90°) – заданный треугольник.

АС = 15 см, СВ = 8 см,

О – центр вписанной окружности. Так как

 АС ˃ СВ, то  ∠ В ˃ ∠ А,

поэтому  ОВ – искомое расстояние.

Если точки  М, N  и  К – точки касания вписанной окружности до сторон треугольника, то по свойству касательной, проведенной до окружности из одной точки, получим:  СN = СК.

Фигура  СNОК – квадрат. Тогда  СN = СК = r.

S_∆ACB = ¹/₂ AC ∙ CB =

= ¹/₂ ∙ 15 ∙ 8 = 60 (см²).

P_∆ACB = 8 + 15 + 17 = 40 (см).

Тогда

ВК = СВ – СК = 8 – 3 = 5 (см).

ОТВЕТ:  √͞͞͞͞͞34 см  

ЗАДАЧА:

Вписанная в прямоугольный треугольник  АВС  окружность касается гипотенузы  АВ  в точке  К. Найдите площадь треугольника, если

АК = 4 см, ВК = 6 см.

РЕШЕНИЕ:

Пусть окружность  О  радиуса  х  касается катетов треугольника в точках  М  и  N.

Так как  ОМСN – квадрат, то  СМ = СN = х см. По свойству касательных, проведённых из одной точки, получим:

АN = АК = 4 см,

ВМ = ВК = 6 см.

Рассмотрим прямоугольный треугольник  АВС.

В нём:

АВ = 4 + 6 = 10 (см),

АС = (4 + х) см,

ВС = (6 + х) см.

По теореме Пифагора имеем:

АС² + ВС² = АВ²,

(4 + х)² + (6 + х)² = 10²,

2х² + 20х + 52 = 100,

х² + 10х – 24 = 0,

х₁ – не подходит, х₂ = 2. Откуда 

АС = 4 + х = 4 + 2 = 6 (см),

ВС = 6 + х = 6 + 2 = 8 (см).

Тогда 

S = ¹/₂ AC ∙ BC =

= ¹/₂ ∙ 6 ∙ 8 = 24 (см²).

ОТВЕТ:  24 см²

ЗАДАЧА:

Биссектриса прямого угла прямоугольного треугольника делит гипотенузу на отрезки длиной  3 см  и  4 см. Найдите радиус окружности, вписанной в треугольник.

РЕШЕНИЕ:

Пусть  АВС – заданный прямоугольный треугольник (∠ А = 90°),

в котором  АР – биссектриса, ВР = 4 см, РС = 3 см. Биссектриса угла треугольника делит противоположную сторону на отрезки, пропорциональные двум другтм сторонам:

АС : АВ = СР : РВ = 3 : 4.

 Пусть  АС = 3х см.

Тогда  АВ = 4х см.

По теореме Пифагора

ВС² = АВ² + АС²,

(4 + 3)² = 16х² + 9х²,

25х² = 49, х² = ⁴⁹/₂₅,

х₁ = 1,4, х₂ = –1,4 – не подходит. Тому 

АС = 3 ∙ 1,4 = 4,2 (см),

АВ = 4 ∙ 1,4 = 5,6 (см).

S = ¹/₂ AB∙ AC, S = pr, где

r – радиус вписанной окружности, откуда

ОТВЕТ:  1,4 см

ЗАДАЧА:

Найдите площадь прямоугольного треугольника, гипотенуза которого  на  7 см  больше одного из катетов, а другой катет равен  21 см.

РЕШЕНИЕ:

Начертим чертёж.

АС² + СВ² + АВ², 

х² + 21² = (х + 7)²,

х² + 441 = х² + 14х + 49,

14х = 392, х = 28 (см).

S = ¹/₂ AС∙ ВC,

S = ¹/₂ 28 ∙ 21 = 294 (см²).

ЗАДАЧА:

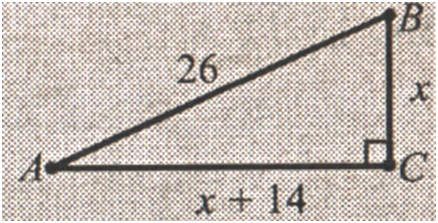
Найдите площадь прямоугольного треугольника, гипотенуза которого равна  26 см, а один из катетов на  14 см  больше второго.

РЕШЕНИЕ:

Начертим чертёж.

х² + (х + 14)² = 26²,

2х² + 28х – 480 = 0,

х² + 14х – 240 = 0,

х₁ = 10, х₂ = –24 – не подходит.

АС = 10 + 14 = 24 (см).

S = ¹/₂ AС∙ ВC =

= ¹/₂ 24 ∙ 10 = 120 (см²).

ЗАДАЧА:

Один из катетов прямоугольного треугольника равен  15 см, а медиана, проведённая до гипотенузы, – 8,5 см. Найдите площадь данного треугольника.

РЕШЕНИЕ:

Начертим чертёж.

ЗАДАЧА:

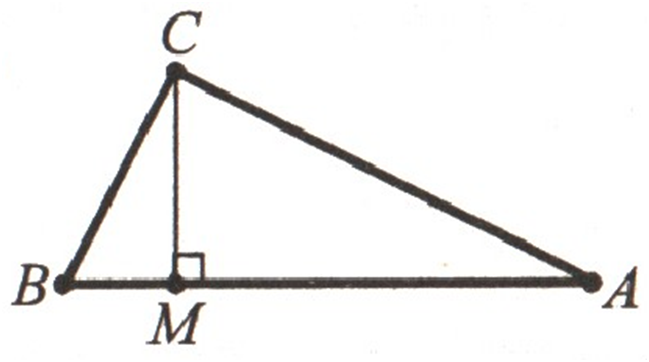
Перпендикуляр, опущенный из вершины прямого угла на гипотенузу прямоугольного треугольника, делить этот треугольник на два треугольника, площади которых равны  1,5 см²  и  13,5 см². Найдите стороны данного треугольника.

РЕШЕНИЕ:

Пусть  АВС – заданный прямоугольный треугольник,

∠ С = 90°, СМ ⊥ АВ,

S_∆CMB = 1,5 см²,

S_∆AMC = 13,5 см².

Пусть  СМ = х см. Тогда:

S_∆CMB = ¹/₂ CM ∙ MB, откуда

Аналогично  S_∆AMC = ¹/₂ CM ∙ AM, откуда

По свойству высоты прямоугольного треугольника, опущенной на гипотенузу, получим:

х₁ = 3, х₂ = –3 – не подходит.

Поэтому,

МВ = 3 : х = 3 : 3 = 1 (см),

АМ = 27 : х = 27 : 3 = 9 (см).

АВ = АМ + ВМ = 9 + 1 = 10 (см).

Из треугольника  АСМ:

Из треугольника  ВСМ:

ОТВЕТ:

3√͞͞͞͞͞10 см, √͞͞͞͞͞10 см, 10 см.

Задания к уроку 5

• Задание 1
• Задание 2
• Задание 3

Другие уроки:

• Урок 1. Единицы измерения площади
• Урок 2. Площадь прямоугольника
• Урок 3. Площадь квадрата
• Урок 4. Площадь треугольника
• Урок 6. Площадь равнобедренного треугольника
• Урок 7. Площадь параллелограмма
• Урок 8. Площадь ромба
• Урок 9. Площадь трапеции
• Урок 10. Площадь равнобедренной трапеции
• Урок 11. Площадь прямругольной трапеции
• Урок 12. Площадь круга и его частей
• Урок 13. Подобие разносторонних треугольников
• Урок 14. Подобие равнобедренных треугольников
• Урок 15. Подобие прямоугольных треугольников
• Урок 16. Площадь многоугольника