среда, 8 марта 2017 г.

Урок 3. Графіки

На координатній площині можна наочно зобразити залежність між різними величинами.

ПРИКЛАД:

Відстані від часу.

Температури від часу.

Для цього на площині наносяться осі координат: горизонтальна – вісь абсцис та вертикальна – вісь ординат. По осі абсцис відкладаються у певному масштабі різні значення аргументу x, або абсциси різних точок графіка, по осі ординат – відповідні їм значення функції у, або ординати точок графіка. Кожна пара координат, абсцису та ордината, дає одну точку графіка. Графік будується за знайденими характерними точками і з урахуванням виявлених загальних властивостей залежних величин і кривих графіка на різних ділянках Неперервна лінія, що з’єднує ці точки, називається графіком залежності величин. Для контролю правильності побудови графіка додатково обчислюють координати однієї або декількох контрольних точок і наносять їх на графік. Контрольні точки служать також уточнення кривих графіка окремих ділянках. За графіком можна знаходити відповідні значення величин, аналізувати.

ПРИКЛАД:

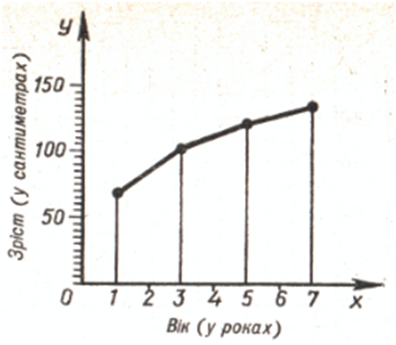
Коли Марійці минув рік, зріст її становив  70 см, коли їй було  3 роки – 100 см, 5 років – 120 см  і  7 років – 135 см. За цими даними можна побудувати діаграму.
На діаграмі не повністю видно, як змінювався зріст Марійки: вона росла весь час, а на діаграмі видно її зріст тільки у віці  1, 3, 5  і  7 років. Сполучивши верхні кінці стовпчиків відрізками, дістанемо ломану лінію, яка краще показує, як змінювався зріст Марійки.
Ми бачимо, що в  4 роки її зріст приблизно дорівнював  110 см, а в  6,5 років – 132 см.
Якби зріст Марійки вимірювали весь час, то утворилася б не ламана, а плавна лінія, ображена на малюнку.
За цією лінією можна дізнатися про зріст Марійки в будь-який момент часу від  1  до  7 років. Так, у  2 роки її зріст був  90 см. Таку лінію називають графіком зросту Марійки.
Щоб якнайточніше будувати графіки, їх креслять на міліметровому папері. Наприклад, графік зросту Марійки на міліметровому папері показано на малюнку.
Графіками користуються для зображення руху.

 ПРИКЛАД:

Нехай поїзд, що йде з швидкістю  60 км/год, вийшов о  3 год  ранку з міста Ромська. Тоді о  4 год  ранку він буде на відстані  60 км  від Ромська, а о  5 год  ранку – на відстані  120 км  від нього і так далі. Подана нижче таблиця показує відстань поїзда від Ромська в різні моменти часу.
Позначимо пари чисел  (3; 0), (4; 60), (5; 120),  тощо точками на координатній площині. При цьому буде зручніше вибирати різні масштаби на осях координат. Позначимо на осі абсцис одиницю відрізком завдовжки  1 см, а на осі ординат – 60 одиниць відрізком завдовжки  1 см. Дістанемо точки  А, В, С, D, Е, F  і  Н.
Усі ці точки лежать на одній прямій.
 Якщо поїзд не вийшов з Ромська о  3 год ранку, а пройшов мимо нього в цей час, то таблицю можна продовжити і вліво:
Знак <<мінус>> показує, що поїзд ще не дійшов до міста Ромська, а йде до нього. Точки з координатами  (0; –180), (1; –120), (2; –60)  лежать на одній прямій з раніше знайденими. Цю пряму називають графіком руху поїзда. За графіком можна дознатися, де був поїзд о  5 год 30 хв (він відійшов од м. Ромська на  150 км), де він був о  1 год 30 хв (він не дійшов од м. Ромська на  90 км), коли він відійшов од м. Ромська на  270 км (о  7 год 30 хв)  тощо.

ПРИКЛАД:

Ви знаєте, що вартість товару залежить від його кількості: що більшу кількість товару купують, то більшою буде його вартість. Наприклад, якщо ціна одного кілограма цукерок становить  35 грн, то за  2 кг  треба заплатити  70 грн, за  3 кг – 105 грн  тощо. Ви знаєте, що таку відповідність можна наочно відобразити на діаграмі.

Проте за діаграмою важко визначити, скільки коштує  2,5 кг  цукерок або інша їх кількість. Зобразимо дані про вартість цукерок не стовпчиками, а вертикальними відрізками в системі координат. Оскільки величина  << маса цукерок >>  і  << вартість покупки >>  є прямо пропорційними, то верхні кінці стовпчиків діаграми можна з’єднати відрізками. Вона показує, як змінюється вартість покупки залежно від маси цукерок. Таку лінію називають графіком залежності величини  << вартість покупки >>  від величини << маса цукерок >>.
ПРИКЛАД:

Між пристанями  А  і  В, розташованими на протилежних берегах озера, курсує пором. На рисунку зображено графік руху порома під час двох перших рейсів від  А  до  В  і назад. З якою швидкістю здійснював пором другий рейс з  А  до  В ?
З графіку видно, що відстань від пристані  А  до пристані  В  дорівнює  8 км. Першим рейсом пором проплив  від  пристані  А  до пристані  В  за  40 хв, потім стояв біля пристані  В  40 хв, після чого через  40 хв  повернувся до пристані  А. Другим рейсом пором з  А  до  В  проплив за 

 (240 – 160 = 80) хв.

Означає швидкість його була:

 8 км : 80 хв = 0,1 км/хв, або
0,1 км/хв × 60 хв = 6 км/год.          

 Завдання до уроку 3
Інші уроки:
Автор: на

Комментариев нет:

Отправить комментарий

Подписаться на: Комментарии к сообщению (Atom)