Исследуя поведение функции вблизи некоторой точки, удобно пользоваться
понятиям окрестности.
Окрестностью точки а называется любой
интервал, который содержит эту точку.
ПРИМЕР:
Интервал
(2; 6) – один из окрестностей точки 3.
Интервал
(–3,3; –2,7) – окрестность точки –3.
ПРИМЕР:
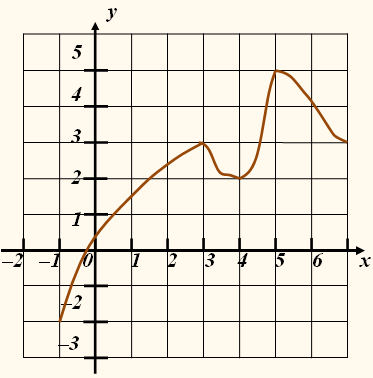
Изучая график рисунка, можно
прийти к выводу, что <<самыми заметными>> точками области
определения являются такие точки х,
в которых рост функции изменяется падением (точки 3 и 5) или, наоборот, падение
изменяется ростом (точка 4).
ПРИМЕР:
Функция, которая представлена
графически на рисунку, на сегменте
[–3; 6]
имеет наибольшее значение в
точке х = 1 и наименьшее – в точке х = 6.
Дадим точное определение точек экстремума.
ОПРЕДЕЛЕНИЕ:
Точка х0 называется точкой минимума функции f,
если для всех х из некоторой окрестности х0 выполняется неравенство
f(x) ≥
f(х0).
Минимум функции – это значение функции в такой её точке, в которой оно
является наименьшим в любой, сколь угодно малой окрестности этой точки.
Значение
уmin = f(хmin)
называется минимумом
функции.
ОПРЕДЕЛЕНИЕ:
Точка х0 называется точкой максимума функции f,
если для всех х из некоторой окрестности х0 выполняется неравенство
f(x) < f(х0).
По определению значение функции f
в точке максимума х0 будет наибольшим среди
значений функции из некоторой окрестности этой точки, поэтому график функции в окрестности х0, как правило, имеет вид гладенького
<<горба>> (рис. 4), или
заострённого <<пика>> (рис.
3).
Максимум функции
– это её значение в такой точке, в которой оно является наибольшим в любой
сколь угодно малой окрестности этой точки.
Значение
уmax = f(хmax)
называется
максимумом функции.
Другие примеры поведения
графиков функции в точках приведены ниже.
а – точка максимумаа – точка минимума
Тут каждая точка промежутка (–1; 0) будет как точкою минимума, так и точкой максимума.
Для точек максимума и минимума функции принято общее название – их называют
точками экстремума.
Значение функции в этих точках называют соответственно максимумами и минимумами
функции (общее название – экстремум функции). Точки максимума обозначают хmax, а точки минимума хmin. Значения функции в этих точках обозначают соответственно уmax и
уmin.
хmax – точка
максимума
уmax – максимум
хmin – точка
минимума
уmin – минимум
хmax, хmin – точки
экстремума
уmax, уmin – экстремумы
Функция f(x) в точке х = с имеет максимум (минимум), если в области определения
её можно указать такой интервал, для которого
с будет внутренней точкой и для всех отличных от с точек х этого интервала
f(x) < f(c)
[f(x) > f(c)].
Из этого определения выходит, что значение функции в крайних точках области
её определения может быть наибольшим или наименьшим, но не может быть ни
максимумом, ни минимумом.
ПРИМЕР:
Определите точки экстремума
функции
ПРИМЕР:
Построить график линейной функции и назвать наибольшее и
наименьшее значение функции.
у =
–2х + 1,
х ∈ [–3; 2].
унаим =
–3.
ПРИМЕР:
Построить график линейной функции и назвать наибольшее и
наименьшее значение функции.
у =
–2х + 1,
х ∈ (–3; 2).
ПРИМЕР:
Какое наибольшее значение приобретает функция ?
f(x) = –9х2 – 6х + 19.
РЕШЕНИЕ:
–9х2 – 6х + 19 =
= –(3х + 1)2 + 20.
Данная
функция приобретает наибольшее значение, когда
3х + 1 = 0.
Это
значение равно 20.
ПРИМЕР:
Какое наименьшее значение приобретает функция ?
f(x) = 9х2 – 18х – 1.
РЕШЕНИЕ:
9х2 – 18х – 1 =
= 9х2 – 18х + 9 – 10 =
= (3х – 3)2 – 10.
Данное
выражение приобретает наименьшее значение, когда
3х – 3 = 0.
Это
значение равно –10.
ПРИМЕР:
Какое наибольшее значение приобретает функция ?
f(x) = 4х3 – х6
+ 1.
РЕШЕНИЕ:
f(x) = 4х3 – х6 + 1 =
= –х6 + 4х3 – 4 + 5 =
= –(х3 – 2)2 + 5.
Первое слагаемое
преобразованной функции меньше или равно 0 для всех х, поэтому
наибольшее значение функция приобретает при
Другие уроки:
- Урок 1. Координатная плоскость
- Урок 2. Диаграммы
- Урок 3. Графики
- Урок 4. Множества
- Урок 5. Что такое функция ?
- Урок 6. Аналитический способ задания функции
- Урок 7. Табличный способ задания функции
- Урок 8. Графический способ задания функции
- Урок 9. Нахождение области определения и области значения функции аналитическим методом
- Урок 10. Нахождение области определения и области значения функции с помощью графика
- Урок 11. Нули функции
- Урок 12. Возрастание и убывание функции
- Урок 14. Симметричные функции
- Урок 15. Чётные и нечётные функции
- Урок 16. Функция, обратная данной
- Урок 17. Линейная функция
- Урок 18. График линейной функции
- Урок 19. Прямая пропорциональность
- Урок 20. График прямой пропорциональности
- Урок 21. Взаимное расположение графиков линейных функций
- Урок 22. Функция обратно пропорциональной зависимости
- Урок 23. График функции обратно пропорциональной зависимости
- Урок 24. Квадратичная функция
- Урок 25. График функции у = aх2 + b
- Урок 26. График функции у = a(х - m)2 + n
- Урок 27. График функции у = aх2 + bx + c
- Урок 28. Функция y = √͞͞͞͞͞х и её график
- Урок 29. Функция y = хn и её график
- Урок 30. Построение графиков функций методом геометрических преобразований









Комментариев нет:
Отправить комментарий