Урок 27. График функции у = aх2 + bx + c

вторник, 10 июля 2018 г.

Урок 27. График функции у = aх2 + bx + c

Выясним, что представляет собой график квадратичной функции. Мы установили, что график функции, заданной уравнением

у = a(х – b)² + c,

является образом графика функции

у = ах²

при параллельном переносе, отображающем начало координат на точку О^’(b; c).

Всякую квадратичную функцию можно задать уравнением вида:

у = a(х – b)² + c.

Следовательно,

График функции

у = aх² + bx + c

есть парабола, конгруэнтная параболе

у = aх².

Осью симметрии является прямая

Если а < 0, то ветки параболы направлены вниз и значение

будет наибольшим значением функции, если а > 0, то ветки параболы направлены вверх и значение

будет наименьшим значением функции.

Если D < 0, то парабола не пересекает ось абсцисс, если D = 0, то парабола касается оси х вершиной, если D ˃ 0 , то парабола пересекает ось х в точках:

Парабола пересекает ось у в точке с координатами (0; с).

Если квадратный трёхчлен aх² + bx + c имеет два корня х₁ и х₂, то парабола пересекает ось абсцисс в двух точках с координатами (х₁; 0), (х₂; 0).

Если квадратный трёхчлен aх² + bx + c имеет единственный корень х₁, то парабола имеет с осью абсцисс единственную общую точку с координатами (х₁; 0).

Если квадратный трёхчлен aх² + bx + c не имеет корней, то парабола не имеет с осью абсцисс общих точек.
Нули функции у = aх² + bx + c.

Значения аргумента, при которых значения функции у = aх² + bx + c равны нулю, являются корнями квадратного трёхчлена aх² + bx + c. Можно определить нули функции и на графике этой функции.

ПРИМЕР:

Найдите нули функции:

у = 3х² – 7x + 4.

РЕШЕНИЕ:

Аналитический способ.

Найдём корни уравнения

3х² – 7x + 4 = 0.

Графический способ.

Построим график функции

у = 3х² – 7x + 4.

Из графика видно, что функция обращается в нуль при

х = 1 и х = 1¹/₃.

ПРИМЕР:

Найдите нули функции:

у = 6х² – x.

РЕШЕНИЕ:

Аналитический способ.

Найдём корни уравнения

6х² – x = 0.

Графический способ.

Построим график функции

у = 6х² – x.

Из графика видно, что функция обращается в нуль при
х = 0 и х = ¹/₆.

ПРИМЕР:

Пусть требуется построить график функции, заданной уравнением:

у = ¹/₂ х² – 8х + 35.

РЕШЕНИЕ:

Представим это уравнение в другом виде, выделив из трёхчлена квадрат двучлена. Получим уравнение

у = ¹/₂ (х – 8)² + 3.

Выясним, что представляет собой график этого уравнения.

Вычислим координаты нескольких точек, принадлежащих этому графику.

Легко видеть, что наименьшее значение, равное 3 функция принимает при х = 8. Если значение х отличается от 8 на одно и тоже число, то соответствующее им значения у равны. Например, если х = 6, то у = 5, и если х = 10, то у = 5.

Построив точки, координаты которых указаны в таблице, и соединив их плавной линией, получим график функции

у = ¹/₂ (х – 8)² + 3.

Следовательно, график функции

у = ¹/₂ (х – 8)² + 3

есть парабола, являющаяся образом параболы

у = ¹/₂ х²

при параллельном переносе, который начало координат отображает на точку с координатами

(8; 3).

ПРИМЕР;

Построить график функции

у = 2х² + 4х – 1.

Графиком этой функции является парабола. Найдём координаты её вершины. Для этого можно, выделив из трёхчлена квадрат двучлена, представить уравнение

у = 2х² + 4х – 1.

в виде

у = 2(х + 1)² – 3.

Отсюда ясно, что вершина параболы – точка с координатами

(–1; –3).

Построив в координатной плоскости вершину параболы – точку с координатами

(–1; –3)

и зная, что осью симметрии параболы служит прямая

х = –1

и что <<ветви>> параболы направлены вверх, мы можем представить себе общий вид графика функции

у = 2х² + 4х – 1.

Для построения графика вычислим координаты нескольких точек, принадлежащих этому графику:

Построив в координатной плоскости точки, координаты которых занесены в таблицу, и соединив их плавной линией, мы получим график функции

у = 2х² + 4х – 1.

ПРИМЕР:

Постройте график функции:

у = –х² – 6х – 5.

Используя график, найдите:

– множество значений функции;

– промежуток, на котором функция падает.

РЕШЕНИЕ:

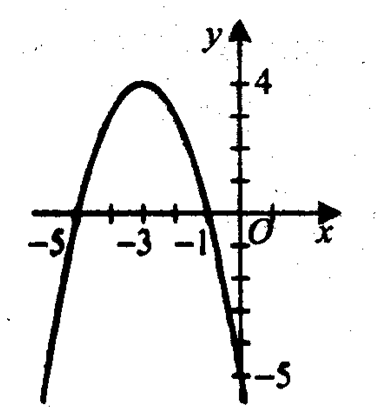
Графиком функции у = –х² – 6х – 5 является парабола, ветви которой направлены вниз. Найдем координаты вершины параболы:

Точка (–3; 4) является вершиной данной параболы. Найдем абсциссы точек пересечения графика функции с осью Ох:

–х² – 6х – 5 = 0,

х₁ = –5, х₂ = –1.

График этой функции пересекает ось ординат в точке (0; –5).

Построим график заданной функции.

Из рисунка видно, что:

1) множеством значений функции является промежуток (–∞; 4].

2) функция спадает на промежутке [–3; +∞).

ОТВЕТ:

множеством значений функции является промежуток (–∞; 4],

функция падает на промежуток [–3; +∞)

ПРИМЕР:

Постройте график функции

у = –х² + 4х + 5.

Используя график, найдите:

– множество значений функции;

– промежуток, на котором функция падает.

РЕШЕНИЕ:

Данная функция является квадратичной функцией, график парабола, ветви которой направлены вниз.

Абсцисса вершины параболы:

Ордината вершины:

Найдем точки пересечения параболы осью абсцисс:

–х² + 4х + 5 = 0,

х² – 4х – 5 = 0

х₁ = –1, х₂ = 5.

Таким образом, парабола пересекает ось абсцисс в точках

(0; –1) и (0; 5).

Найдем точку пересечения парабол с осью ординат:

у(0) = 5.

Парабола пересекает ось ординат в точке (0; 5).

Используя найденные четыре точки параболы, выполним ее построение.

График данной функции изображен на рисунке.
ОТВЕТ:

область значений функции есть промежуток (–∞; 9],

функция падает на промежутке [2; +∞)

ПРИМЕР:

Постройте график функции:

РЕШЕНИЕ:

Областью определения данной функции есть все действительные числа, кроме числа 0. Тогда на области определения:

Графиком этой функции является парабола, ветви которой направлены вверх

(а = 1 ˃ 0).

Координаты вершины:

Парабола пересекает ось х в точках с абсциссами –3 и 1.

График заданной функции есть парабола

у = x² + 2x – 3 без точки (0; –3).

ПРИМЕР:

Постройте график функции:

РЕШЕНИЕ:

Графиком этой функции является парабола, ветви которой направлены вверх

(а = 1 ˃ 0).

Координаты вершины:

Парабола пересекает ось х в точках с абсциссами –3 и 1.

График заданной функции есть парабола

у = x² + 2x – 3 без точки (0; –3).

ПРИМЕР:

Постройте график и укажите область значений функции

у = –х² – 2х + 3.

РЕШЕНИЕ:

Графиком функции у = –х² – 2х + 3 является парабола, направленная ветвями вниз.

Поэтому значение в ее вершине является наибольшим, которого она достигает. Координаты вершины:

поэтому областью значений функции есть промежуток (–∞; 4].

ПРИМЕР:

Постройте график и укажите область значений функции

f(x) = х² + 8х – 3.

РЕШЕНИЕ:

Графиком функции f(x) = х² + 8х – 3 является парабола, направленная ветвями вверх.
Найдем ее вершину:

поэтому областью значений функции является промежуток [–19; +∞).

ПРИМЕР:

Найдите ординату вершины параболы, фрагмент которой изображен на рисунке.

РЕШЕНИЕ:

Абсциссы х₁ = 0, х₂ = 4 – нули квадратичной функции, поэтому

у = а(х – х₁)(х – х₂) =

= а(х – 0)(х – 4) = ах² – 4ах.

Парабола проходить через точку (1; 3). Поэтому,

3 = а – 4а = –3а, а = –1.

у = –х² + 4х.

Абсцисса вершины параболы
Ордината
ОТВЕТ: 4

ПРИМЕР:

Постройте график функции:

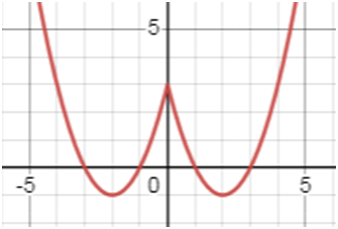
у = х² – 4|х| + 3.

РЕШЕНИЕ:

По определению модуля получим:

1) если х ≥ 0, то у = х² – 4х + 3 и графиком функции является часть параболы, ветви которой направлены вверх (а = 1 ˃ 0).

Координаты вершины
Парабола пересекает ось х в точках с абсциссами 1 и 3, а ось ординат – в точке (0; 3).

2) если х < 0, то у = х² + 4х + 3 и графиком функции является часть параболы, ветви которой направлены вверх (а = 1 ˃ 0).

Координаты вершины

Парабола пересекает ось х в точках с абсциссами –1 и –3, а ось ординат – в точке (0; 3).

Задания к уроку 27

Другие уроки:

Уроки математики и физики для школьников и родителей

вторник, 10 июля 2018 г.