Объемом геометрического тела называется величина части пространства, занимаемого этим телом.
Принято рассматривать объём как величину, обладающую следующими свойствами:
– равные тела имеют равные объёмы;
Применение тригонометрических функций для решения стереометрических задач.
ЗАДАЧА:
Основанием прямой призмы является параллелограмм со сторонами
9 см и 14 см
и углом между ними 30º. Высота призмы – 15 см. Найдите объём призмы.
= 945 (см3).
ОТВЕТ:
945 см3.
Дана прямая четырёхугольная призма АС1, у которой
и двугранный угол AA1OO1DD1= α. Найти объём призмы.
РЕШЕНИЕ:
определим по данным площадям диагональных сечений
Угол AOD = α как линейный угол данного двугранного угла. Тогда площадь четырёхугольника ABCD
Откуда найдам
Определим объём:
ОТВЕТ: ЗАДАЧА:
В основании прямой призмы лежит треугольник с углами α и β. Диагональ боковой грани, которая содержит сторону, для которой данные углы будут прилежащими, равна d и образует с плоскостью основания угол γ. Найдите объём призмы.
РЕШЕНИЕ:
Пусть в основании прямой призмы АВСА1В1С1 лежит треугольник АВС, в котором
∠ А = α, ∠ В = β.
Тогда данная диагональ грани
АА1В1В, А1В = d.
Поскольку ребро АА1 перпендикулярно плоскости АВС, то проекция диагонали А1В на эту плоскость будет сторона АВ треугольника АВС. Поэтому по условию задачи
∠ А1ВА = γ.
Объём призмы
V = S × h.
AA1 = d sin γ, AB = cos γ.
В основании прямой призмы лежит равнобедренный треугольник. Две диагонали смежных боковых граней, которые имеют общую вершину, равны l и образуют между собой угол α. Плоскость, которая проходит через эти диагонали, наклонена к плоскости основания под углом β. Найдите объём призмы.
РЕШЕНИЕ:
Пусть в основании прямой призмы
АВСА1В1С1
лежит равнобедренный треугольник
АВС (АВ = ВС).
V = Sосн × H.
Высота В1N равнобедренного треугольника АВ1С будет его биссектрисою и медианою.
Тогда:
Sосн = 1/2×AC×BN = AN×BN =
ОТВЕТ:
1/4 l3×sin α×cos α/2×sin 2β.
Основание прямой призмы – ромб со стороною а и тупым углом α. Через большую диагональ нижнего основания и вершину тупого угла верхнего основания проведена плоскость, которая образует с плоскостью основания угол β. Найдите объём призмы.
РЕШЕНИЕ:
∠ BAD = ∠ BCD =
α.
Тогда
ВD – большая диагональ. Треугольник ВDС1 –
данное сечение. По свойству диагоналей ромба
СО ⊥ ВD. По теореме про три перпендикуляра С1О ⊥ ВD. Тогда ∠ С1ОС – угол, который образуется плоскостью сечения с плоскостью
основания.
По условию, ∠ С1ОС = β.
Из ∆ AOD (∠ O = 90º):
∠ A = α/2,
OA = AD cos ∠ A = a cos α/2,
OC = OA = a cos α/2.
Из ∆ OCC1 (∠ C = 90º):
OC1 = OC tg ∠ O = a cos α/2 tg β.
V = Sосн. ∙ H = SABCD ∙ CC1 =
= a2 sin α ∙ a cos α/2 tg β =
= a3 sin α cos α/2 tg β.
ОТВЕТ: a3 sin α cos α/2 tg β
ЗАДАЧА:
Основание прямой призмы – ромб с большею диагональю d и острым углом α. Через меньшую диагональ нижнего основания и вершину острого угла верхнего основания проведена плоскость, которая образует с плоскостью основания угол γ. Найдите объём призмы.
РЕШЕНИЕ:
∠ BCD =
α, АС = d.
Треугольник ВС1D –
данное сечение.
∠ ОCD = ∠ ОCВ =
α/2.
Так как СО ⊥ ВD (как диагонали ромба), то по теореме про три перпендикуляра ОС1 ⊥ ВD. Тогда ∠ С1ОC – угол, который образуется плоскостью сечения и плоскостью основания. По условию, ∠ С1ОC = γ.
Из ∆ СOD (∠ O = 90º):
OD = OC tg ∠ C = d/2 tg α/2,
BD = 2OD = d tg α/2.
Из ∆ OCC1 (∠ C = 90º):
OC1 = OC tg ∠ O = d/2 tg γ.
SABCD = 1/2×AC×BD =
= 1/2×d×d tg
α/2 = 1/2×d2×tg
α/2.
V = Sосн.∙ H = SABCD ∙ CC1 =
= 1/2×d2× tg
α/2× d/2 tg γ =
ОТВЕТ:
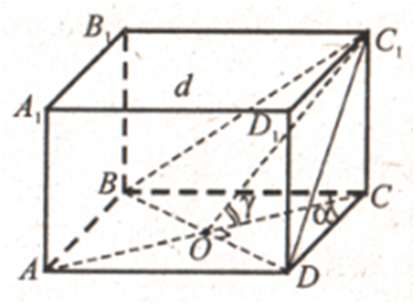
ЗАДАЧА:Найдите
объём четырёхугольной прямой призмы, высота которой равна h,
диагонали наклонены к плоскости основания под углами α и β, а острый угол между диагоналями
основания равен γ.
РЕШЕНИЕ:
Надо найти объём призмы АВСDА1В1С1D1.
Так как высота призмы дана, то решение
сводится к отысканию площади её основания
АВСD, которое является выпуклым четырёхугольником.
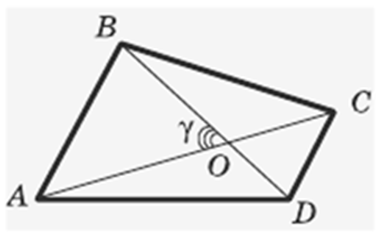
Площадь выпуклого четырёхугольника
выражается через его диагонали d1, d2 и угол между ними γ по формуле:
S = 1/2 d1d2 sin γ.
C1C и D1D перпендикулярны плоскости основания. ∠ С1АС
= α, ∠D1DВ = β. Из треугольников
АСС1 и ВDD1 находим диагонали основания:
d1 = AC = h∙ ctg α,
d2 =
BD = h∙ ctg β.
Vпризмы = SABCD∙ h =
- Урок 1. Единицы измерения объёмов
- Урок 3. Объём наклонной призмы
- Урок 4. Объём правильной призмы
- Урок 5. Объём прямого параллелепипеда
- Урок 6. Объём наклонного параллелепипеда
- Урок 7. Объём прямоугольногопараллелепипеда
- Урок 8. Объём куба
- Урок 9. Объём пирамиды
- Урок 10. Объём правильной пирамиды
- Урок 11. Объём усечённой пирамиды
- Урок 12. Объём цилиндра
- Урок 13. Объём конуса
- Урок 14. Объём усечённого конуса
- Урок 15. Объём шара и его частей
- Урок 16. Тела вращения
- Урок 17. Комбинации тел (2)
- Урок 18. Правильные многогранники
- Урок 19. Объёмы подобных тел















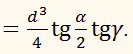


Комментариев нет:
Отправить комментарий