Графиком функции
у = х2.
у = х2.
будет кривая линия, которая называется параболою. Область определения –
множество всех действительных чисел. Составим таблицу значений функции для некоторых
значений аргумента х:
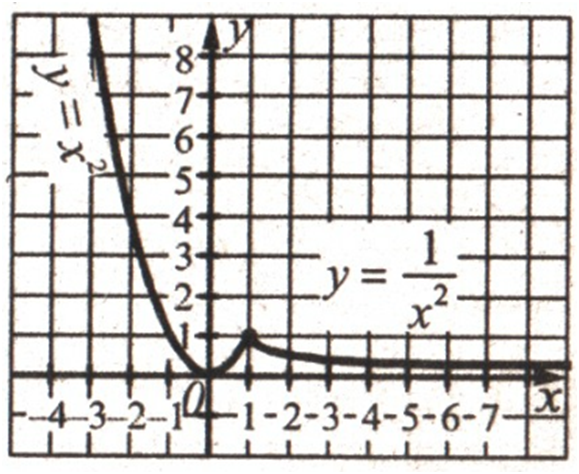
Если бы на координатной плоскости обозначили больше точек с координатами х и у, которые соответствуют формуле у = х2, они разместились бы так, как показано на рисунку.
Когда для каждого действительного значения х в формуле у = х2 вычислили соответствующее значение у и обозначили точки с этими координатами на координатной плоскости то получили бы такой график
Точка с координатами (0; 0) делит параболу на две равные части, каждую из которых называют веткой параболы, а саму точку – вершиной параболы.
Построенный график
даёт возможность наглядно определить свойства функции.
– если х
= 0, то и у
= 0 (график проходит через точку 0(0; 0));
– при всех значениях
х значения функции неотрицательные (ниже оси
х нет ни одной точки графика);
– противоположным значениям аргумента соответствуют равные
значения функции (график симметричный относительно оси у);
– когда х
< 0, функция уменьшается
(её график <<идёт вниз>>), а когда
х ˃ 0,
функция растёт (её график направлен вверх).
Квадратичная
функция вида
у =
aх2.
Также чётная,
неограниченная, определённая для всех действительных х.
Её график также парабола, проходящая через начало координат и симметричная оси
ординат. Но при положительных значениях а ветви её
направлены вверх, а при а
< 0 – вниз. Чем меньше
абсолютная величина а, тем дальше отходят ветки параболы от оси ординат, тем
<<шире>> она.
График функции у = aх2
+ b.
Рассмотрим
преобразование графика функции у = f(х).
Это построение графика функции
у = f(х) + n.
График
функции у = f(х) + n получается из
графика функции у = f(х)
с
помощью параллельного переноса вдоль оси ординат на n единиц. Вверх при n > 0 и вниз при
n < 0.
ПРИМЕР:
Построим график функции
у = –х2 – 2.
РЕШЕНИЕ:
График функции
у = –х2 – 2.
Получается из графика функции
у = –х2.
Параллельным переносом вдоль оси ординат на 2 единицы вниз, т. к.
n = –2 < 0.
ПРИМЕР:n = –2 < 0.
Построим график функции
у = 2х2 + 4.
РЕШЕНИЕ:
Это значит, что парабола, которая является графиком функции
у = 2х2,
перемещается на четыре единицы вверх по оси у. При этом все значения у увеличиваются на 4.
Таблица значений
у = 2х2.
у = 2х2 + 4.
Мы видим по таблице, что вершина параболы второй функции на 4 единицы выше вершины параболы первой (её координаты (0; 4)). А значения у второй функции на 4 больше значений у первой функции.
Графиком функции
у =
aх2 + b
является параболой,
которую можно получить из графика функции
у =
aх2
с помощью
параллельного переноса вдоль оси у на b единиц вверх, если b > 0,
или на –b единиц вниз,
если b
< 0.
ОДЗ: (–∞;
0) ∪ (0; + ∞).
Постройте график функции:РЕШЕНИЕ:
ОДЗ: (–∞; 0) ∪ (0; + ∞).
Постройте график функции:РЕШЕНИЕ:
ОДЗ: (–∞; 0) ∪ (0; + ∞).
Тогда:
Учитывая определение модуля, будем иметь: 1) если х ˃ 0, то |х| = х, 2) если х < 0, то |х| = –х,Поэтому,Точка пересечения с осью Ох:у = 0,
–х2
+ 2 = 0, х = –√͞͞͞͞͞2.
Постройте график функции:РЕШЕНИЕ:
ОДЗ: (–∞; 0) ∪ (0; + ∞).
Постройте график функции:Пользуясь построенным графиком, найдите
промежутки роста и убывания функции.
Искомый график на рисунке.ОТВЕТ: промежуток роста: [0; 1],
(–1; 1).ПРИМЕР:
РЕШЕНИЕ:
При х ≤ 1 графиком
функции будет часть параболы
у
= х2
с промежутком убывания (–∞; 0] и промежутком роста [0; 1].
Искомый график на рисунке.ОТВЕТ: промежуток роста: [0; 1],
промежутки убывания (–∞; 0] и (1; +∞):
ПРИМЕР:
(–1; 1).ПРИМЕР:
Областью определения
функцииесть
все действительные числа.Графиком данной функции является парабола
у = х2 – 1.ПРИМЕР:
у = х2 – 1.ПРИМЕР:
Областью определения
функцииесть
все действительные числа, кроме чисел –2 и 2. ТогдаГрафиком данной функции является парабола
у = х2 + 4
Постройте график функции:РЕШЕНИЕ:Данное
уравнение равносильно системеПоэтому
графиком данной функции является парабола
у = – х2 без точки (1;
–1).ПРИМЕР:
Постройте график функции:РЕШЕНИЕ:
Областью определения функцииесть все действительные числа, кроме чисел –2 и 2. ТогдаГрафиком данной функции является парабола
Областью определения функцииесть все действительные числа, кроме чисел –2 и 2. ТогдаГрафиком данной функции является парабола
у = х2 + 1
Другие уроки:
- Урок 1. Координатная плоскость
- Урок 2. Диаграммы
- Урок 3. Графики
- Урок 4. Множества
- Урок 5. Что такое функция ?
- Урок 6. Аналитический способ задания функции
- Урок 7. Табличный способ задания функции
- Урок 8. Графический способ задания функции
- Урок 9. Нахождение области определения и области значения функции аналитическим методом
- Урок 10. Нахождение области определения и области значения функции с помощью графика
- Урок 11. Нули функции
- Урок 12. Возрастание и убывание функции
- Урок 13. Экстремальные значения функции
- Урок 14. Симметричные функции
- Урок 15. Чётные и нечётные функции
- Урок 16. Функция, обратная данной
- Урок 17. Линейная функция
- Урок 18. График линейной функции
- Урок 19. Прямая пропорциональность
- Урок 20. График прямой пропорциональности
- Урок 21. Взаимное расположение графиков линейных функций
- Урок 22. Функция обратно пропорциональной зависимости
- Урок 23. График функции обратно пропорциональной зависимости
- Урок 24. Квадратичная функция
- Урок 26. График функции у = a(х - m)2 + n
- Урок 27. График функции у = aх2 + bx + c
- Урок 28. Функция y = √͞͞͞͞͞х и её график
- Урок 29. Функция y = хn и её график
- Урок 30. Построение графиков функций методом геометрических преобразований






















































Комментариев нет:
Отправить комментарий