Графиком линейной функции является прямая.
y = аx + b.
Это прямая,
параллельная прямой, служащей графиком y
= аx, и проходящая
через точку (0; b) на оси ординат.
Построить график функции:
у = –0,5х + 4.
РЕШЕНИЕ:
у = –0,5х + 4
Все отмеченные точки лежат на одной прямой.эта прямая является графиком линейной функции
ПРИМЕР:
Какая из точек принадлежит графику функции ?
у = 3 – 4х
А(0; 4), B(1; 3),
C(1; –1), D(3; 2).
РЕШЕНИЕ:
Графику функции у = 3 – 4х принадлежит точка С(1; –1), так
как
–1 = 3 – 4 ∙ 1,
ПРИМЕР:
Укажите уравнение прямой, параллельной оси ординат.
х + у = 1,
х – у = 1,
х – 1 = 0,
у + 1 = 0.
РЕШЕНИЕ:
Параллельной оси ординат является прямая
х – 1 = 0.
ПРИМЕР:
у = ах + b, а = tg 120° = –√͞͞͞͞͞3 ,
у = –√͞͞͞͞͞3х +b , 0 = –√͞͞͞͞͞3 ∙ 2 + b, b = 2√͞͞͞͞͞3,
у = –√͞͞͞͞͞3 x + 2√͞͞͞͞͞3 .
ПРИМЕР:
Через какую из точек проходит график функции
у = 0,8х + 4 ?
А(0; 4), B(1; 3),
C(5; 8), D(3; 2).
РЕШЕНИЕ:
Через точку C(5; 8), ибо если х = 5, то
у = 0,8 ∙ 5
+ 4 = 8, 8 = 8.
ПРИМЕР:
Найдите точку пересечения графика функции
у = 5х – 20
с осью ординат.
РЕШЕНИЕ:
х = 0, у = 5 ∙ 0 – 20 = –20,
поэтому точка пересечения (0; –20).
ПРИМЕР:
Через какую точку проходит график уравнения ?
у =
3х – 4.
РЕШЕНИЕ:
Через точку C(1; –1), ибо если х = 1, то
у = 3 ∙ 1
– 4 = –1, 8 = 8.
ПРИМЕР:
Постройте график функции:
|х + у|
= 4.
РЕШЕНИЕ:
Используя определение модуля, получим:
1) если х + у
≥ 0, у ≥ –х, то
х + у = 4, у = –х
+ 4
и графиком этой функции является прямая, проходящая через
точки (0;
4) и (4; 0).
2) если х + у
< 0, у < –х, то
х + у = –4, у = –х
– 4
Постройте график функции:
|х – у|
= 3.
РЕШЕНИЕ:
Используя определение модуля, получим:
1) если х – у
= 3, у = х – 3.
Графиком этой функции является прямая, проходящая через
точки (0; –3) и (3; 0).
2) если х – у
= –3, у = х + 3, то
.ПРИМЕР:
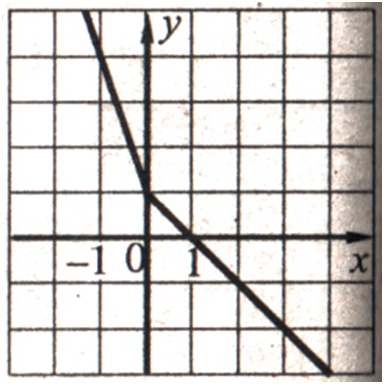
Постройте график функцииРЕШЕНИЕ:График функции изображен на рисунке.Функция возрастает на промежутку (–∞; +∞), промежутков убывания нет.- Урок 1. Координатная плоскость
- Урок 2. Диаграммы
- Урок 3. Графики
- Урок 4. Множества
- Урок 5. Что такое функция ?
- Урок 6. Аналитический способ задания функции
- Урок 7. Табличный способ задания функции
- Урок 8. Графический способ задания функции
- Урок 9. Нахождение области определения и области значения функции аналитическим методом
- Урок 10. Нахождение области определения и области значения функции с помощью графика
- Урок 11. Нули функции
- Урок 12. Возрастание и убывание функции
- Урок 13. Экстремальные значения функции
- Урок 14. Симметричные функции
- Урок 15. Чётные и нечётные функции
- Урок 16. Функция, обратная данной
- Урок 17. Линейная функция
- Урок 19. Прямая пропорциональность
- Урок 20. График прямой пропорциональности
- Урок 21. Взаимное расположение графиков линейных функций
- Урок 22. Функция обратно пропорциональной зависимости
- Урок 23. График функции обратно пропорциональной зависимости
- Урок 24. Квадратичная функция
- Урок 25. График функции у = aх2 + b
- Урок 26. График функции у = a(х - m)2 + n
- Урок 27. График функции у = aх2 + bx + c
- Урок 28. Функция y = √͞͞͞͞͞х и её график
- Урок 29. Функция y = хn и её график
- Урок 30. Построение графиков функций методом геометрических преобразований


















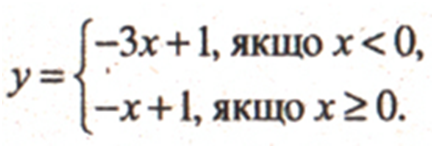




Комментариев нет:
Отправить комментарий