Урок 20. График прямой пропорциональности

четверг, 22 июня 2017 г.

Урок 20. График прямой пропорциональности

Прямая пропорциональность является частным случаем линейной функции, так как формула у = kх получается из формулы

у = kх + b

при b = 0.

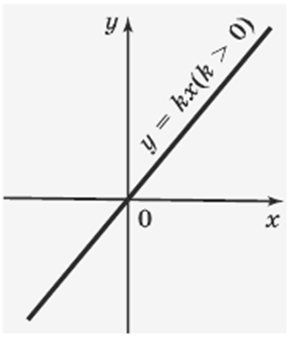
Отсюда следует, что графиком прямой пропорциональности служит прямая. Эта прямая проходит через начало координат, так как при

х = 0

значение у равно 0.

Графиком прямой пропорциональности является прямая, проходящая через начало координат.

На рисунке

изображён график функции у = kх при k ˃0, а на рисунке

– график функции у = kх при k <0.

Порядок построения графика прямой пропорциональности:

– выбрать произвольное значение аргумента, отличного от нуля;

– вычислить соответствующее значение функции при выбранном аргументе;

– отметить на координатной плоскости полученную точку;

– провести прямую через начало координат и полученную точку.

ПРИМЕР:

Построить график функции

у = 0,5х.

РЕШЕНИЕ:

Здесь множество значений переменной х – множество всех чисел. Соответствие между множеством значений переменной х и множеством значений переменной у является прямой пропорциональностью с коэффициентом пропорциональности, равным 0,5.

Построим график рассматриваемой функции. Для этого составим таблицу:

Построим точки, координаты которых помещены в таблице.
Можно заметить, что точки расположены по прямой, проходящей через начало координат. Проведём эту прямую.
Построенная прямая является графиком функции у = 0,5х, заданной на множестве всех чисел. Её т также графиком прямой пропорциональности, заданной формулой у = 0,5х на множестве всех чисел.

Тем же способом можно построить график функции у = –2х.

Этот график также является прямой линией и проходит через начало координат.

Для построения графика прямой пропорциональности достаточно отметить какую-либо точку графика, отличную от начала координат, и провести через точку и начало координат прямую.

ПРИМЕР:

Построить график функции

у = 2х.

РЕШЕНИЕ:

Графиком этой функции является прямая, проходящая через начало координат. Для его построения достаточно найти одну точку графика, отличную от начала координат, и провести прямую через начало координат и найденную точку.

В качестве такой точки выберем точку (1; 2) (если х = 1, то у = 2 ∙ 1 = 2).

График функции у = 2х изображён на рисунке.

Расположение графика функции у = kх в координатной плоскости зависит от коэффициента k. Из формулы у = kх находим, что если х = 1, то у = k. Значит, график функции у = kх проходит через точку (1; k). При k > 0 эта точка расположена в первой координатной четверти, а при k < 0 – в четвёртой. Отсюда следует, что при k > 0 график прямой пропорциональности расположен в первой и третьей координатных четвертях.

ПРИМЕР:

y = 0,5x.

А при k < 0 – во второй и четвёртой.

ПРИМЕР:

у = –1,5х.

На рисунке построены графики прямой пропорциональности при различных значениях k.

ПРИМЕР:

Построить график функции:

у = |х|.

РЕШЕНИЕ:

Это уравнение распадается на два:

1) у = х при х ≥ 0,

2) у = –х при х ≤ 0.

График этой функции состоит из двух полупрямых.

Так как у ≥ 0, то оси координат можно вычерчивать только для верхней полуплоскости.

у(–х) = |–х| = |х| = у(х),

следовательно, функция чётная. Поэтому вычерчиваем только прямую ветвь (при х ≥ 0), представляющую собой прямую у = х. Левая ветвь её симметрична.

ПРИМЕР:

Построить график функции:

|у| = х.

РЕШЕНИЕ:

Область существования функции х ≥ 0, так как |у| – число неотрицательное.

График симметричен относительно х-ов, так как |у| = |–у|.

При у ≥ 0 имеем полупрямую у = х.

При у ≤ 0 имеем полупрямую, ей симметричную относительно горизонтальной оси.
Если область определения функции у = kх состоит не из всех чисел, то её графиком служит подмножество точек этой прямой (например, луч, отрезок, отдельные точки.).

ПРИМЕР:

Известно, что график прямой пропорциональности проходит через точку А(5; 22). Проходит ли этот график через точку В(7; 32,4) ?

РЕШЕНИЕ:

Точка А определяет коэффициент пропорциональности: