График функции, заданной формулой
где k ≠ 0
где k ≠ 0
(на множестве всех чисел, отличных от нуля), есть кривая линия, состоящая из двух ветвей.
Кривую такого вида
называют гиперболой
или равносторонней гиперболой.
Она симметрична относительно начала
координат, так как функция
у =
k/х
Если область определения функции состоит из всех отличных от нуля чисел, то её графиком служит подмножество точек этой гиперболы (одна её ветвь, отдельные точки и т. д.).
ПРИМЕР:
Построим график функции
Сначала построим ветвь графика на промежутке (0; +∞). Составим таблицу значений функции:Нанесём полученные точки на координатную плоскость и соединим их плавной кривой.Это и будет ветвь графика функции у = 1/х на промежутке (0; +∞).
Воспользовавшись нечётностью функции у = 1/х, добавим к построенной
ветви ветвь, симметричную ей относительно начала координат. Получим график
функции у = 1/х:ПРИМЕР:Сначала построим ветвь графика на промежутке (0; +∞). Составим таблицу значений функции:Нанесём полученные точки на координатную плоскость и соединим их плавной кривой.Это и будет ветвь графика функции у = 1/х на промежутке (0; +∞).
Пусть функция задана формулой
Построим график рассматриваемой функции.
При х
= 0 функция
Найдём значения у,
соответствующие некоторым положительным значениям х и некоторым отрицательным значениям х:
Например,
если х
= 120,
то у
= 0,1,
если х
= 2400,
то у
= 0,005.
Достаточно малым значениям х соответствуют большие значения у.
Например,
если х
= 0,03,
то у
= 400.
Отрицательным значениям
х соответствуют
отрицательные значения у. Точки
графика с отрицательными координатами симметричны относительно начала координат
точкам графика с положительными координатами. В координатной плоскости отметим
все точки, координаты которых помещены в таблице.
График функции, заданной формулой
на множестве всех чисел, кроме нуля, состоит из двух ветвей, расположенных в первом и третьем координатных углах. Его называют графиком обратной пропорциональности, рассматриваемой на множестве всех отличных от нуля чисел, с коэффициентом обратной пропорциональности, равным 12.
ПРИМЕР:
На рисунке построен график функции
График обратно
пропорциональной зависимости есть кривая линия, состоящая из двух отдельных ветвей,
расположенных в первом и третьем координатных углах при k ˃ 0
ПРИМЕР:
у =
1/х
ПРИМЕР:
у =
– 1/х
ПРИМЕР:
При каких значениях
k график функции
у = k/x
проходит через точку
А(2/7; –14) ?
РЕШЕНИЕ:
ПРИМЕР:
РЕШЕНИЕ:
График функции состоит из части гиперболы у = – 2/х для х ≤ –1 и
части прямой у = 1 – х для х
˃ –1.
Областью определения
функции есть все действительные числа, кроме чисел 0 и 1.Графиком
данной функции является гипербола у = –2/х без точки (1;
–2).ПРИМЕР:
Областью определения
функции есть все действительные числа, кроме числа –1.Графиком
данной функции является гипербола, полученная параллельным переносом гиперболы у = 6/х на 1 единицу влево и на 4 единицы вверх.ПРИМЕР:
Областью определения
функции есть все действительные числа, кроме чисел 0 и 3.Графиком
данной функции является гипербола у = 6/х без точки (3; 2).ПРИМЕР:
Областью определения
функции есть все действительные числа, кроме чисел 0 и 1.Графиком
данной функции является гипербола у = – 8/х без точки (1;
–8).ПРИМЕР:
Постройте график функции:Используя график, найдите промежутки роста и промежутки
убывания функции.
ПРИМЕР:
РЕШЕНИЕ:
График функции состоит из части гиперболы у = 6/х для х < –1 и х
˃ 1 та части прямой у
= 6х для –1 ≤ х ≤ 1.
ПРИМЕР:
Областью определения
функции есть все действительные числа, кроме чисел 0 и 3.Графиком
данной функции является гипербола у = –5/х без точки (3; –12/3).ПРИМЕР:
Областью определения
функции есть все действительные числа, кроме числа 3.Графиком
данной функции является гипербола, полученная параллельным переносом гиперболы у = –6/х на 3 единицы вправо и на 2 единицы вверх.ПРИМЕР:
Постройте график функции:Используя график, найдите промежутки роста и промежутки
убывания функции.
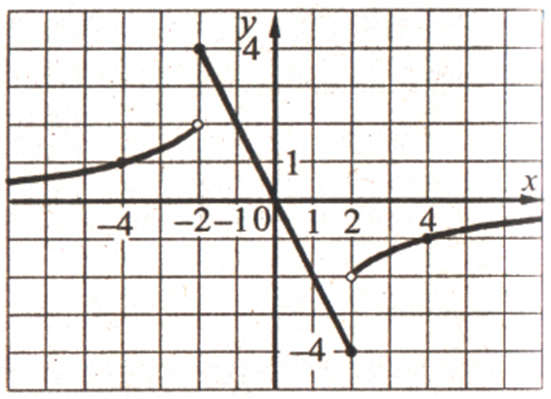
РЕШЕНИЕ:
График функции состоит из части гиперболы у = –4/х для х < –2 и х
˃ 2 и части прямой у
= –2х для –2 ≤ х ≤ 2.
Другие уроки:
- Урок 1. Координатная плоскость
- Урок 2. Диаграммы
- Урок 3. Графики
- Урок 4. Множества
- Урок 5. Что такое функция ?
- Урок 6. Аналитический способ задания функции
- Урок 7. Табличный способ задания функции
- Урок 8. Графический способ задания функции
- Урок 9. Нахождение области определения и области значения функции аналитическим методом
- Урок 10. Нахождение области определения и области значения функции с помощью графика
- Урок 11. Нули функции
- Урок 12. Возрастание и убывание функции
- Урок 13. Экстремальные значения функции
- Урок 14. Симметричные функции
- Урок 15. Чётные и нечётные функции
- Урок 16. Функция, обратная данной
- Урок 17. Линейная функция
- Урок 18. График линейной функции
- Урок 19. Прямая пропорциональность
- Урок 20. График прямой пропорциональности
- Урок 21. Взаимное расположение графиков линейных функций
- Урок 22. Функция обратно пропорциональной зависимости
- Урок 24. Квадратичная функция
- Урок 25. График функции у = aх2 + b
- Урок 26. График функции у = a(х - m)2 + n
- Урок 27. График функции у = aх2 + bx + c
- Урок 28. Функция y = √͞͞͞͞͞х и её график
- Урок 29. Функция y = хn и её график
- Урок 30. Построение графиков функций методом геометрических преобразований















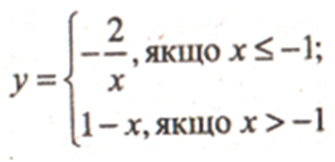
















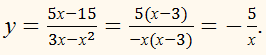


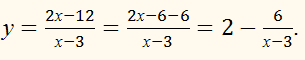


Комментариев нет:
Отправить комментарий