Для того щоб графічно вирішити систему двох рівнянь
із двома змінними, потрібно в одній системі координат побудувати графіки
рівнянь. Графічне рішення системи лінійних рівнянь із двома змінними зводиться
до пошуку координат загальних точок двох прямих ліній. Як відомо, дві прямі на
площині можуть бути паралельними або такими, що перетинаються. У разі
паралельності прямі або мають спільних точок, або збігаються. Якщо кутові
коефіцієнти прямих, які є графіками рівнянь системи, різні, то прямі
перетинаються. Координати точки їх перетину є рішенням цієї системи, і до того
ж єдиним.
Системі двох рівнянь першого ступеня із двома
невідомими в декартовій системі координат відповідає пара прямих. Оскільки дві
прямі на площині можуть перетинатися, збігатися чи бути паралельними, те й
відповідна їм система рівнянь може мати одне рішення, нескінченну кількість
розв'язків або жодного. Вирішити систему рівнянь із двома невідомими можна
графічно.
ПРИКЛАД:
2х +
3y = 5,
а
координати будь-якої точки прямої СD є рішенням рівнянн
3x – y = –9.
Координати
точки перетину прямих задовольняють як першому рівнянню, і другому, т. е. є
рішенням системи. Графіки перетинаються у точці К(–2; 3). Отже, система має єдине рішення:
х
= –2; у = 3.
Застосований нами спосіб розв'язання системи рівнянь
називається графічним. Зауважимо, що графічний спосіб зазвичай дозволяє
знаходити рішення лише приблизно.
Розглянемо системи двох лінійних рівнянь із двома
змінними, у кожному з яких хоча б один із коефіцієнтів при змінних відмінний
від нуля. З'ясуємо, чи завжди така система має рішення і якщо має, скільки.
Графіки рівнянь системи є прямі. Якщо ці прямі перетинаються, система має єдине
рішення; якщо прямі паралельні, система не має рішень; якщо прямі збігаються,
то рішень нескінченно багато.
ПРИКЛАД:
у = –1,1х + 12,
у = –6x + 18
задаються
лінійні функції. Кутові коефіцієнти прямих, є графіками цих функцій, різні.
Отже, ці прямі перетинаються, і система має єдине рішення.
ПРИКЛАД:
у = –0,4х + 0,15
у = –0,4x + 3,2
паралельні,
тому що їх кутові коефіцієнти однакові, а точки перетину з віссю у різні.
Звідси випливає, що ця система рівнянь немає рішень.
ПРИКЛАД:
Розв'яжіть графічно систему рівнянь:
Для цього побудуємо на одній координатній площині графіки обох її рівнянь.
Координати кожної точки прямої, яка є графіком рівняння
(–2; –6), (–1; –4,5), (0; –3), (1; –1,5), (2; 0), …
– розв'язок даної системи рівнянь.
Є й такі системи рівнянь, які не мають жодного розв'язку. Графіки таких рівнянь – паралельні прямі.
ПРИКЛАД:
Побудуємо
пряму – графік рівняння 3х + 2y = 5 – за двома точками, наприклад (1;
1) та (3; –2).
- Урок 1. Лінійне рівняння з одним невідомим і цілими вільними членами
- Урок 2. Лінійне рівняння з одним невідомим і дрібними вільними членами
- Урок 3. Застосування правил визначення невідомого доданка, зменшуваного і від'ємника для розв'язання задач
- Урок 4. Застосування правил визначення невідомого множника для розв'язання задач
- Урок 5. Розв'язування рівнянь, що зводяться до лінійних
- Урок 6. Розв'язування рівнянь із змінною в знаменнику
- Урок 7. Застосування правил визначення діленого і дільника для розв'язання задач
- Урок 8. Лінійне рівняння з двома невідомими
- Урок 9. Рішення лінійних рівнянь за допомогою графіків
- Урок 10. Лінійне рівняння з параметром
- Урок 11. Системи двох рівнянь першого степеня з двома невідомими
- Урок 12. Розв'язання систем рівнянь способом підстановки
- Урок 13. Розв'язання систем рівнянь способом алгебраїчного додавання
- Урок 15. Розв'язування задач за допомогою систем лінійних рівнянь
- Урок 16. Системи трьох лінійних рівнянь з трьома невідомими
- Урок 17. Повне квадратне рівняння загального вигляду
- Урок 18. Зведене квадратне рівняння
- Урок 19. Теорема Вієта
- Урок 20. Неповні квадратні рівняння
- Урок 21. Розв'язання квадратного рівняння способом виділення квадрата двочлена
- Урок 22. Графічний спосіб розв'язування квадратних рівнянь
- Урок 23. Квадратний тричлен
- Урок 24. Квадратні рівняння з параметрами
- Урок 25. Дробові раціональні рівняння
- Урок 26. Задачі на складання квадратних рівнянь
- Урок 27. Рівняння кола
- Урок 28. Системи рівнянь другого степеня є двома невідомими
- Урок 29. Розв'язування задач за допомогою систем рівнянь другого степеня
- Урок 30. Перетин прямої з колом
- Урок 31. Рішення нелінійних систем рівнянь за допомогою графіків
- Урок 32. Системи рівнянь з параметрами
- Урок 33. Рівняння вищих степенів
- Урок 34. Розв'язання рівнянь способом заміни
- Урок 35. Розв'язання систем рівнянь способом заміни
- Урок 36. Задачі на знаходження чисел
- Урок 37. Задачі на знаходження цифр
- Урок 38. Рішення задач на змішування за допомогою рівнянь
- Урок 39. Рішення задач на змішування за допомогою систем рівнянь
- Урок 40. Ірраціональні рівняння










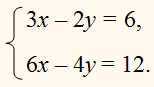





Комментариев нет:
Отправить комментарий