понедельник, 10 октября 2016 г.

Урок 9. Рішення лінійних рівнянь за допомогою графіків

Кожна пара чисел, що є розв'язком рівняння зі змінними  х  і  у, зображується в координатній площині точкою, координатами якої служить ця пара чисел (абсцисою є значення  х, а ординатою – значення  у). Усі такі точки утворюють графік рівняння.

Графіком рівняння із двома змінними називається безліч точок координатної площини, координати яких є рішеннями цього рівняння.

Нехай дано рівняння з двома змінними  f(х; у) = 0. Якщо всі його рішення зобразити точками на координатній площині, то вийде кілька точок площини. Цю множину називають графіком рівняння  f(х; у) = 0.

Наприклад,

Графіком рівняння  у – х2 = 0  є парабола  у = х2.

Графіком рівняння  у – х = 0  є пряма (бісектриса першого та третього координатних кутів).

Графіком рівняння  у – 3 = 0  є пряма, паралельна до осі  х.
Графіком рівняння  х + 2 = 0 – пряма паралельна осі  у.
Графіком рівняння
є одна точка  (1; 2), оскільки координати цієї точки задовольняють цьому рівнянню.

Алгоритм побудови графіка рівняння  аx + by = c.

– вибрати будь-яке зручне значення змінної  х = х1  і з рівняння  аx + by = c  обчислити значення  у = у1;

– вибрати інше значення змінної  х = х2  і з рівняння  аx + by = c обчислити значення  у = у2;

– на координатній площині відзначити точки  (х1; у1), (х2; у2);

– через точки провести пряму – вона є шуканим графіком.

ПРИКЛАД:

Зобразіть розв'язки лінійного рівняння

–х + у – 2 = 0

точками координатної площині  хОу.

РОЗВ'ЯЗАННЯ:

Нескладно підібрати кілька рішень:

(3; 5), (2; 4), (1; 3), (0; 2), (–2; 0).

Побудуємо ці точки в координатній площині та переконаємося, що вони лежать на одній прямій.
Ця пряма є графіком рівняння

–х + у – 2 = 0.

ПРИКЛАД:

Накреслити графік рівняння

х – 2у – 4 = 0.

РОЗВ'ЯЗАННЯ:

Підставимо  х = 0  у рівняння, отримаємо:

0 – 2у – 4 = 0,

–2у = 4,  у = – 2.

Підставимо  у = 0  у рівняння, отримаємо:

х – 2 ∙ 0 – 4 = 0,

х – 4 = 0,  х = 4.

Зазначимо отримані точки  (0; –2)  і  (4; 0)  у прямокутній системі координат.

Проведемо через ці точки пряму лінію.
Вона і буде графіком лінійного рівняння

х – 2у – 4 = 0.

ПРИКЛАД:

Побудувати графік рівняння

2х – 3у = –6.

РОЗВ'ЯЗАННЯ:

Графік цього лінійного рівняння є пряма. Для побудови прямої достатньо знати дві її точки.

Підставивши в рівняння

2х – 3у = –6

замість  x  значення  0, отримаємо  –3у = –6, звідки  у = 2.

Підставивши в рівняння

2х – 3у = –6

замість значення  0, отримаємо  2х = –6, звідки  х = –3.

Отже, ми знайшли дві точки графіка:

(0; 2)  і  (–3; 0).

Провівши через них пряму лінію, отримаємо графік рівняння

2х – 3у = –6.
ПРИКЛАД:

З'ясуємо, що є графік рівняння:

3x + 2y = 6.

Виразимо змінну  у  через  х:

у = – 1,5х + 3.

Цією формулою задається лінійна функція, графіком якої є пряма.
Оскільки рівняння

3x + 2y = 6 

у = – 1,5х + 3

рівносильні, то ця пряма є і графіком рівняння

3x + 2y = 6.

Графіком будь-якого лінійного рівняння

аx + by = c,

у якого хоча б один із коефіцієнтів при змінних відмінний від нуля, є пряма лінія.

Якщо  b = 0, то ця пряма паралельна до осі  у.

Якщо  а = 0, то ця пряма паралельна до осі  х.

ПРИКЛАД:

Розглянемо рівняння:

2x + 0y = 8.

РОЗВ'ЯЗАННЯ:

Його рішеннями служать усі пари чисел  (х; у), у яких  х = 4, а  у – будь-яке число, наприклад  (4; 2), (4; 0), (4; –4,5). Графік рівняння складається з усіх точок, абсцис яких дорівнює  4, а ордината – довільному числу. Такі точки утворюють пряму, що проходить через точку  (4; 0)  та паралельну осі  у.
Графіком лінійного рівняння з двома змінними, у якому хоча б один із коефіцієнтів при змінних не дорівнює нулю, є пряма.

ПРИКЛАД:

Побудуємо графік рівняння:

3x – 4y = 12.

РОЗВ'ЯЗАННЯ:

У цьому рівнянні коефіцієнти при змінних відмінні від нуля. Тому її графіком є пряма. Пряма визначається двома точками. Знайдемо координати двох будь-яких точок прямої:

якщо  х = 0,  то  у = –3; 

якщо  х = 2,  то  у = –1,5. 

Зазначимо точки  (0; –3)  і  (2; –1,5)  і проведемо через них пряму.
Ця пряма – графік рівняння

3x – 4y = 12.

Розглянемо тепер випадок, як у лінійному рівнянні обидва коефіцієнта при змінних дорівнюють нулю.

Рівняння  ax + by = c, в якому обидва коефіцієнти при змінних дорівнюють нулю, має вигляд

0 ∙ х – 0 ∙ у = с,

При  c = 0  будь-яка пара чисел є розв'язком цього рівняння, яке графіком – вся координатна площину.

При  c ≠ 0  рівняння немає рішень і його графік не містить жодної точки.

 ПРИКЛАД:

Знайдіть безліч точок координатної площини  хОу, координати  х, у  яких задовольняють рівняння:

2х2 – 8х + у2 + 6у + 17 = 0.

РОЗВ'ЯЗАННЯ:

Це рівняння має єдине рішення:

х = 2,  у = –3,

тобто даному рівнянню задовольняють координати лише однієї точки  М(2: –3).

ПРИКЛАД:

Знайдіть безліч точок координатної площини  хОу, координати  х, у  яких задовольняють рівняння:

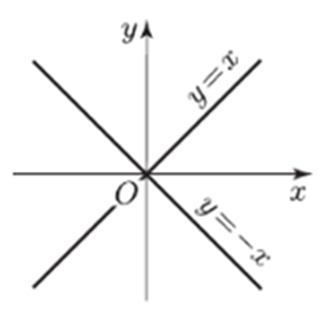
|х| = |у|.

РОЗВ'ЯЗАННЯ:

Рівняння рівносильне сукупності рівнянь

х = у  і  х = –у.

Шукана множина складається з усіх точок, що належать бісектрисам  I  і  III, а також  II  і  IV координатних кутів.
ПРИКЛАД:

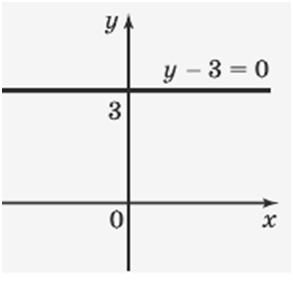
Знайдіть безліч точок координатної площини  хОу, координати  х, у  яких задовольняють рівняння:

х + |у| = 0,

РОЗВ'ЯЗАННЯ:

Рівняння рівносильне сукупності двох систем:
Першою з них задовольняють точки, що належать бісектрисі  II координатного кута, другій системі – точки, що належать бісектрисі  III  координатного кута.
ПРИКЛАД:

Знайдіть безліч точок координатної площини  хОу, координати  х, у  яких задовольняють рівняння:

х2 + 4х + у2 – 6у + 12 = 0.

РОЗВ'ЯЗАННЯ:

Запишемо рівняння у вигляді:

(х2 + 4х + 4) + (у2 – 6у + 9) – 1 = 0,

(х + 2)2 + (у – 3)2 = 1.

Це рівняння кола з центром у точці  А(–2; 3)  та радіусом 1.
Завдання до уроку 9
Інші уроки:
Автор: на

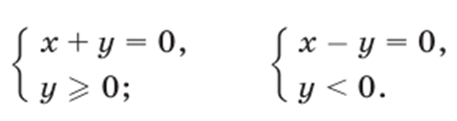
Комментариев нет:

Отправить комментарий

Подписаться на: Комментарии к сообщению (Atom)