Розв’яжемо систему цих рівнянь:
ВІДПОВІДЬ: 9 і 6 кг сіна.
Річковий
пароплав за течією йшов з швидкістю 16 км/год, а проти течії – з
швидкістю 12 км/год. Визначити швидкість
пароплава і швидкість течії річки.
РОЗВ'ЯЗАННЯ:
16
– число, яке виражає суму швидкостей
пароплава і течії річки,
12
– число, що виражає різницю цих швидкостей.
Умову
задачі можна записати так:
х – швидкість руху пароплава,
у – швидкість руху води в річці.
Тоді
з першої частини умови завдання виходить рівняння:
х
+ у = 16,
а
з іншого:
х
– у = 12.
(16 – у) – у
= 12,
4 = 2у, у
= 2.
х
= 16 – у = 16 – 2 = 14.
ВІДПОВІДЬ:
Швидкість
пароплава 14 км/год, швидкість течії річки 2
км/год
ЗАДАЧА:
Вкладник
поклав у банк гроші на два різних рахунки, по одному з яких нараховували 5%
річних, а по другому – 4%, і отримав через рік за двома
вкладами 1160
грн прибутку. Якби внесені на різні
рахунки кошти поміняли місцями, то річний прибуток становив би 1180
грн. Скільки всього грошей було покладено в банк
?
РОЗВ'ЯЗАННЯ:
Нехай
вкладник поклав х грн. на перший рахунок, а на другий – у грн. Через рік з першого рахунку
він отримав 0,05х грн., а з другого – 0,04у грн. відсоткових грошей, що в сумі
становило 1160 грн. Одержимо рівняння:
0,05х + 0,04у = 1160.
Якщо
внесені на різні рахунки кошти поміняти місцями, то одержимо рівняння:
0,04х + 0,05у = 1180.
0,09(х + у)
= 2340,
х
+ у = 26000.
Отже,
вкладник вніс до банку 26000 грн.
ВІДПОВІДЬ: 26000
грн.
ЗАДАЧА:
Два
пішоходи йдуть назустріч один одному з двох пунктів, відстань між якими
дорівнює 30
км. Якщо перший вийде на 2 год раніше другого, то зустріч
відбудеться через 2,5 години після виходу другого. Якщо ж
другий пішохід вийде на 2 год раніше першого, то зустріч відбудеться через 3 год після виходу першого. З якою швидкістю йде
кожен пішохід ?
РОЗВ'ЯЗАННЯ:
Нехай
х
км/год – швидкість першого пішохода, а у
км/год – швидкість другого пішохода. Якщо перший вийде на 2 години
раніше за другу, то, згідно з умовою, він йтиме до зустрічі 4,5 год,
тоді як другий – 2,5 год.
За 4,5
год перший пройде шлях 4,5х км,
а за 2,5 години
другий пройде шлях 2,5 км. Їхня зустріч означає, що
сумарно вони пройшли шлях 30 км, тобто
4,5х + 2,5у = 30 –
перше рівняння.
Якщо
другий вийде на 2 год раніше за першого, то, згідно з умовою, він
йтиме до зустрічі 5 год, тоді як перший – 3 год. Розмірковуючи, як і вище,
перейдемо до другого рівняння:
3х + 5у = 30.
9х + 5у = 60,
Віднімемо
друге рівняння з першого:
9х + 5у – (3х + 5у)
= 60 – 30,
9х + 5у – 3х – 5у
= 30,
9х – 3х = 30, 6х = 30,
х = 5.
Знайдемо
з другого рівняння, попередньо підставивши замість х
число 5:
3 ∙ 5 + 5у =
30,
5у = 30 – 15, у = 3.
ВІДПОВІДЬ: перший
пішохід йде зі швидкістю 5 км/год, а другий – 3
км/год.
ЗАДАЧА:
За 5
кг цукерок і 4
кг печива заплатили 310
грн. Скільки коштує 1 кг
цукерок і скільки 1 кг
печива, якщо 3 кг
цукерок дорожчі за 2 кг
печива на 76 грн
?
РОЗВ'ЯЗАННЯ:
Нехай 1
кг цукерок коштує х
грн., а 1
кг печива – у грн.
Так
як
за
5 кг
цукерок і 4 кг
печива заплатили 310 грн., то перше рівняння буде
наступне:
5х + 4у = 310,
Якщо 3
кг цукерок дорожчі за 2
кг печива на 76
грн., то друге рівняння буде виглядати так:
3х – 2у = 76.
11х = 462,
х = 42.
Знайдемо
з другого рівняння, попередньо підставивши замість х число 42:
3 ∙
42 – 2у = 76,
2у = 126 – 76,
2у = 50, у = 25.
Отже,
1 кг
цукерок коштує 42 грн., а 1
кг печива – 25 грн.
ВІДПОВІДЬ: 42
грн., 25 грн.
ЗАДАЧА:
Із
села А
в село В,
відстань між якими дорівнює 70 км,
виїхав мотоцикліст. За 10
хв до цього назустріч йому із села В виїхав велосипедист, який зустрівся з
мотоциклістом через 1 год після свого виїзду. Знайдіть швидкість
кожного з них, якщо мотоцикліст за 2 год
проїжджає на 104 км
більше, ніж велосипедист за 4 год.
РОЗВ'ЯЗАННЯ:
Нехай х
км/год – швидкість велосипедиста, у
км/год – швидкість мотоцикліста. Велосипедист до зустрічі рухався 1 год,
мотоцикліст – 1
год і
10 хв = 5/6
(год).
Вони проїхали 70 км. Рівняння:
х + 5/6 у = 70,
х + 5у = 420.
За 2
год мотоцикліст проїжджає 2у
км, а велосипедист за 4 год – 4х км.
Рівняння:
2у – 4х = 104,
у
– 2х = 52.
ВІДПОВІДЬ: 10
км/год, 72 км/год
ЗАДАЧА:
З
першого поля зібрали по 40
ц ячменю з гектара, а з другого – 35
ц з гектара. Усього було зібрано 2600 ц. Наступного року урожайність
першого поля збільшилась на 10%, другого – на 20%, а весь зібраний урожай збільшився
на 400 ц. Знайдіть площу кожного поля.
РОЗВ'ЯЗАННЯ:
Нехай х га – площа першого поля, а у га – площа другого поля. Тоді з першого
поля зібрали 40х ц ячменю, із другого – 35у ц. Після збільшення
врожайності з першого поля зібрали
(40 + 0,1 ∙ 40)х ц,
з другого –
(35 + 0,2 ∙ 35)у ц.
–24х – 21у = –1560.
Складемо обидва рівняння і знайдемо х:
–24х – 21у + 22х + 21у = –1560 + 1500,
–24х + 22х = –60, –2х
= –60, х = 30.
Знайдемо
у з першого рівняння, попередньо підставивши
замість х число 30:
8 ∙
30 + 7у = 520,
7у = 520 – 240,
7у = 280, у = 40.
Отже,
площа першого поля становить 30 га, а другого – 40 га.
ВІДПОВІДЬ: 30 га, 40
га
ЗАДАЧА:
х
= 360.
- Урок 1. Лінійне рівняння з одним невідомим і цілими вільними членами
- Урок 2. Лінійне рівняння з одним невідомим і дрібними вільними членами
- Урок 3. Застосування правил визначення невідомого доданка, зменшуваного і від'ємника для розв'язання задач
- Урок 4. Застосування правил визначення невідомого множника для розв'язання задач
- Урок 5. Розв'язування рівнянь, що зводяться до лінійних
- Урок 6. Розв'язування рівнянь із змінною в знаменнику
- Урок 7. Застосування правил визначення діленого і дільника для розв'язання задач
- Урок 8. Лінійне рівняння з двома невідомими
- Урок 9. Рішення лінійних рівнянь за допомогою графіків
- Урок 10. Лінійне рівняння з параметром
- Урок 11. Системи двох рівнянь першого степеня з двома невідомими
- Урок 12. Розв'язання систем рівнянь способом підстановки
- Урок 13. Розв'язання систем рівнянь способом алгебраїчного додавання
- Урок 14. Рішення лінійних систем рівнянь за допомогою графіків
- Урок 16. Системи трьох лінійних рівнянь з трьома невідомими
- Урок 17. Повне квадратне рівняння загального вигляду
- Урок 18. Зведене квадратне рівняння
- Урок 19. Теорема Вієта
- Урок 20. Неповні квадратні рівняння
- Урок 21. Розв'язання квадратного рівняння способом виділення квадрата двочлена
- Урок 22. Графічний спосіб розв'язування квадратних рівнянь
- Урок 23. Квадратний тричлен
- Урок 24. Квадратні рівняння з параметрами
- Урок 25. Дробові раціональні рівняння
- Урок 26. Задачі на складання квадратних рівнянь
- Урок 27. Рівняння кола
- Урок 28. Системи рівнянь другого степеня є двома невідомими
- Урок 29. Розв'язування задач за допомогою систем рівнянь другого степеня
- Урок 30. Перетин прямої з колом
- Урок 31. Рішення нелінійних систем рівнянь за допомогою графіків
- Урок 32. Системи рівнянь з параметрами
- Урок 33. Рівняння вищих степенів
- Урок 34. Розв'язання рівнянь способом заміни
- Урок 35. Розв'язання систем рівнянь способом заміни
- Урок 36. Задачі на знаходження чисел
- Урок 37. Задачі на знаходження цифр
- Урок 38. Рішення задач на змішування за допомогою рівнянь
- Урок 39. Рішення задач на змішування за допомогою систем рівнянь
- Урок 40. Ірраціональні рівняння



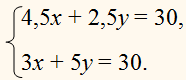






Комментариев нет:
Отправить комментарий