Побудова
графіка квадратичної функції.
ПРИКЛАД:
Побудуйте
графік функції
у
= –х2 – 6х – 5.
Користуючись
графіком, знайдіть:
–
множину значень функції,
–
проміжок, на якому функція спадає.
РОЗВ'ЯЗАННЯ:
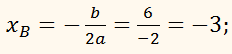
ув = у(–3) = –9 + 18 – 5 = 4.
Точка (–3;
4) є вершиною даної параболи. Знайдемо абсциси
точок перетину графіка функції з віссю Ох:
–х2
– 6х – 5 = 0,
х1 = –5, х2
= –1.
1. Множиною
значень функції є проміжок (–∞; 4].
2. Функція
спадає на проміжку [–3; ∞).
ВІДПОВІДЬ: (–∞; 4], [–3; ∞)
ЗАДАЧА:
Число 60
подайте у вигляді суми двох додатних чисел так, щоб сума їх квадратів була
найменшою.
РОЗВ'ЯЗАННЯ:
Нехай
перше число дорівнює х, тоді друге – 60 – х. Сума квадратів цих чисел
у = х2 + (60 – х)2 =
= 2х2 – 120х + 3600.
60 – 30 = 30.
ВІДПОВІДЬ: 30
і 30
Графічний розв'язок
рівнянь.
Насправді досить часто
виявляється корисним графічний метод розв'язання рівнянь. Він полягає в
наступному: для вирішення рівняння f(x) = 0
будують
графік функції у = f(x) і знаходять абсциси
точок перетину графіка з віссю х
ці
абсциси і є корінням рівняння.
Так, для вирішення
рівняння
aх2
+ bх + c = 0
достатньо побудувати
графік квадратичної функції
у
= aх2 + bх + c
та знайти абсциси точок
перетину цього графіка з віссю х.
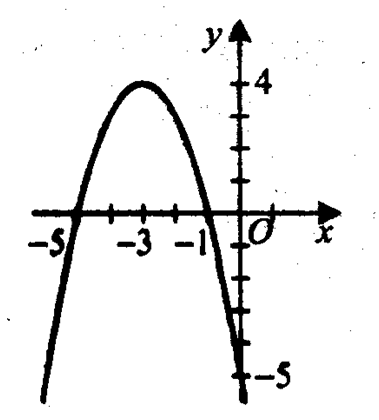
Наприклад, графік
функції
у = –х2 – 6х – 5
перетинає вісь х
у
точках (–5;
0) і (–1; 0),
отже рівняння
–х2 – 6х – 5 =
0
має два корені:
х1 = –5, х2 = –1.
Графік функції у = х2 – 4х + 5 не перетинає вісь абсцис, отже, рівняння х2 – 4х + 5 = 0 не має дійсних коренів.
–3,7 і 0,7.
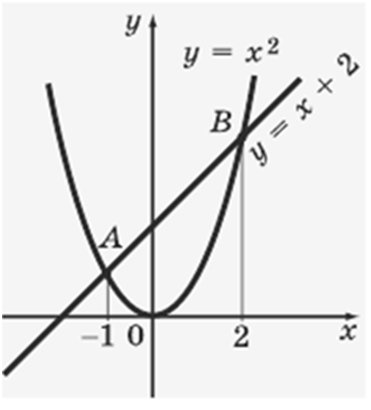
ПРИКЛАД:
Розв'язати
графічно рівняння:
х2
– х – 2 = 0.
РОЗВ'ЯЗАННЯ:
Рівняння
доцільно переписати як
х2
= х + 2.
хА = –1, хВ = 2.
Таким
чином, задане рівняння має два корені –1, 2.
Побудова
графіків за допомогою квадратних рівнянь.
ПРИКЛАД:
= 5х – 1 – х + 3 = 4х + 2.
ПРИКЛАД:
= 5х – 1 – х + 3 = 4х + 2.
ПРИКЛАД:
ПРИКЛАД:
РОЗВ'ЯЗАННЯ:
ПРИКЛАД:
Не
виконуючи побудови, знайдіть координати точок перетину графіків функцій
у = 4/х і у = х – 3.
Накресліть
графіки даних функцій і позначте знайдені точки.
РОЗВ'ЯЗАННЯ:
х(х – 3) = 4,
х2 – 3х – 4
= 0,
х1 = –1, х2
= 4,
ПРИКЛАД:
Не
виконуючи побудови, знайдіть координати точок перетину графіків функцій
у = 8/х і у = х +
2.
Накресліть
графіки даних функцій і позначте знайдені точки.
РОЗВ'ЯЗАННЯ:
х
+ 2 = 8/х,
х(х + 2) = 8,
х2 + 2х – 8
= 0,
х1 = –4, х2
= 2,
ПРИКЛАД:
Не
виконуючи побудови, знайдіть координати точок перетину графіків функцій
у = 6/х і у = 5 – х.
Накресліть
графіки даних функцій і позначте знайдені точки.
РОЗВ'ЯЗАННЯ:
5 – х = 6/х,
х(5
– х) = 6,
х2 – 5х + 6
= 0,
х1 = 2, х2
= 3,
ПРИКЛАД:
Не
виконуючи побудови, знайдіть координати точок перетину графіків функцій
у = 8/х і у = 6 – х.
Накресліть
графіки даних функцій і позначте знайдені точки.
РОЗВ'ЯЗАННЯ:
6 – х = 8/х,
х(6
– х) = 8,
х2 – 6х + 8
= 0,
х1 = 2, х2
= 4,
- Урок 1. Лінійне рівняння з одним невідомим і цілими вільними членами
- Урок 2. Лінійне рівняння з одним невідомим і дрібними вільними членами
- Урок 3. Застосування правил визначення невідомого доданка, зменшуваного і від'ємника для розв'язання задач
- Урок 4. Застосування правил визначення невідомого множника для розв'язання задач
- Урок 5. Розв'язування рівнянь, що зводяться до лінійних
- Урок 6. Розв'язування рівнянь із змінною в знаменнику
- Урок 7. Застосування правил визначення діленого і дільника для розв'язання задач
- Урок 8. Лінійне рівняння з двома невідомими
- Урок 9. Рішення лінійних рівнянь за допомогою графіків
- Урок 10. Лінійне рівняння з параметром
- Урок 11. Системи двох рівнянь першого степеня з двома невідомими
- Урок 12. Розв'язання систем рівнянь способом підстановки
- Урок 13. Розв'язання систем рівнянь способом алгебраїчного додавання
- Урок 14. Рішення лінійних систем рівнянь за допомогою графіків
- Урок 15. Розв'язування задач за допомогою систем лінійних рівнянь
- Урок 16. Системи трьох лінійних рівнянь з трьома невідомими
- Урок 17. Повне квадратне рівняння загального вигляду
- Урок 18. Зведене квадратне рівняння
- Урок 19. Теорема Вієта
- Урок 20. Неповні квадратні рівняння
- Урок 21. Розв'язання квадратного рівняння способом виділення квадрата двочлена
- Урок 23. Квадратний тричлен
- Урок 24. Квадратні рівняння з параметрами
- Урок 25. Дробові раціональні рівняння
- Урок 26. Задачі на складання квадратних рівнянь
- Урок 27. Рівняння кола
- Урок 28. Системи рівнянь другого степеня є двома невідомими
- Урок 29. Розв'язування задач за допомогою систем рівнянь другого степеня
- Урок 30. Перетин прямої з колом
- Урок 31. Рішення нелінійних систем рівнянь за допомогою графіків
- Урок 32. Системи рівнянь з параметрами
- Урок 33. Рівняння вищих степенів
- Урок 34. Розв'язання рівнянь способом заміни
- Урок 35. Розв'язання систем рівнянь способом заміни
- Урок 36. Задачі на знаходження чисел
- Урок 37. Задачі на знаходження цифр
- Урок 38. Рішення задач на змішування за допомогою рівнянь
- Урок 39. Рішення задач на змішування за допомогою систем рівнянь
- Урок 40. Ірраціональні рівняння



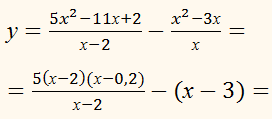















Комментариев нет:
Отправить комментарий