Нехай дано рівність зі змінними х, а:
f(x; a)
= 0.
Якщо ставиться завдання для кожного дійсного
значення а розв'язати це рівняння щодо х, то рівняння f(x; a)
= 0 називають рівнянням зі змінною х
та
параметром а.
aх2 + 2x + 1 = 0.
Якщо a = 1, то
Якщо a < 1, то
kx2 + 12x – 3 = 0
аx2 + 4x + 1 = 0
має два однакові корені ?
ПРИКЛАД:
При
яких значеннях а рівняння не має коренів
?
x2
+ 5aх + 5а = 0.
РОЗВ'ЯЗАННЯ:
Дане рівняння не має коренів, якщо його
дискримінант від’ємний.
x2
+ 5aх + 5а = 0,
D
= (5а)2 – 4∙5a = 25а2 – 20а =
= 5а(5а – 4) < 0, а ∈ (0; 0,8).
ПРИКЛАД:
При
яких значеннях с рівняння не має коренів
?
x2
+ сх + 25 = 0.
РОЗВ'ЯЗАННЯ:
Дане рівняння не має коренів, якщо його
дискримінант від’ємний.
x2
+ сх + 25 = 0,
D
= с2 – 4∙25 = с2 – 100 < 0,
(с – 10)(с + 10) < 0, с ∈ (–10; 10).
ПРИКЛАД:
При
яких значеннях а рівняння не має коренів
?
x2
+ 2ах + 7а = 0.
РОЗВ'ЯЗАННЯ:
Дане рівняння не має коренів, якщо його
дискримінант від’ємний.
x2
+ 2ах + 7а = 0,
D
= (2а)2 – 4∙7a = 4а2 – 28а =
= 4а(а – 7) < 0, а
∈ (0; 7).
ПРИКЛАД:
При
яких значеннях а рівняння не має коренів
?
x2
– х + а – 5 = 0.
РОЗВ'ЯЗАННЯ:
Дане рівняння не має коренів, якщо його
дискримінант від’ємний.
x2
– х + а – 5 = 0,
D
= (–1)2 – 4(а – 5) = 1 – 4а
+ 20 =
= 21 – 4а < 0, 4а
> 21, а > 5,25,
а
∈ (5,25; +∞).
ПРИКЛАД:
При
яких значеннях b рівняння має два різні корені
?
x2
+ bx + 49 = 0.
РОЗВ'ЯЗАННЯ:
Дане рівняння матиме два різні корені,
коли його дискримінант буде додатним.
x2
+ bx + 49 = 0,
D
= b2 – 4∙49 = b2 – 196 > 0,
(b – 14)(b + 14) > 0,
b
∈ (–∞; –14) ∪ (14; +∞).
ПРИКЛАД:
При
яких значеннях b рівняння не має коренів
?
5x2 + bх
+ 20 = 0.
РОЗВ'ЯЗАННЯ:
Дане рівняння не має коренів, якщо його
дискримінант від’ємний.
5x2 + bх
+ 20 = 0,
D
= b2 – 4∙5∙20 = b2 – 400 < 0,
(b – 20)(b + 20) > 0,
b
∈ (–20; 20).
ПРИКЛАД:
Число –3 є коренем рівняння
x2
+ bх – 12 = 0.
Знайдіть
інший корінь рівняння.
РОЗВ'ЯЗАННЯ:
З
теореми Вієта
х1 ∙ х2 = –12, –3х2 = –12, х2 = 4.
ПРИКЛАД:
Число –3 є коренем рівняння
3x2 + 2х + с = 0.
Знайдіть
інший корінь рівняння.
РОЗВ'ЯЗАННЯ:
Оскільки
число –3 є коренем, то воно задовольняє рівняння:
3 ∙ (–3)2 + 2 ∙ (–3) + с = 0,
27
– 6 + с = 0, с = –21.
Рівняння:
3x2 + 2х – 21 = 0,
(3х – 7)(х + 3) = 0,
х1
= –3, х2 = 21/3.
ПРИКЛАД:
Розв'яжіть
рівняння:
(а –1)x2 + 2(2а + 1)х + 4а + 3 = 0.
РОЗВ'ЯЗАННЯ:
Особливо
виділимо значення параметра а = 1. Справа в тому, що при а = 1 дане
рівняння не є квадратним, а при а ≠ 1 воно
квадратне.
Вирішувати
рівняння у кожному з цих випадків треба по-своєму. При а = 1 рівняння
набуває вигляду 6х + 7 = 0, звідки знаходимо
х = –7/6.
Якщо
а ≠ 1 для
квадратного рівняння виділимо ті значення параметра, при яких дискримінант
рівняння обертається в нуль.
Маємо:
D/4 =
5а + 4.
Значить,
а = –4/5.
значення
параметра, на яке нам треба звернути увагу.
Якщо
а < –4/5, D < 0
і,
отже, рівняння немає дійсних коренів.
Якщо
а = –4/5, то D = 0.
а = –4/5, то D = 0.
якщо а < –4/5 то дійсних коренів немає,
якщо а = 1, то х = –7/6,
якщо а = –4/5,
то х = –1/3,
При
якому значенні параметра а рівняння
х2
+ 2(а + 1)х + 9а – 5 = 0
має
два різні негативні корені.
РОЗВ'ЯЗАННЯ:
Оскільки
рівняння повинно мати два дійсні корені х1
і
х2, його дискримінант повинен бути
позитивним. Маємо:
D = 4(а + 1)2
– 4(9а – 5) =
= 4а2 – 28а + 24 = 4(а – 1)(а – 6).
Значить
має виконуватися нерівність:
4(а – 1)(а – 6) ˃ 0.
За
теоремою Вієта для заданого рівняння маємо:
х1 + х2
= –2(а + 1),
х1
х2 = 9а – 5.
Оскільки,
за умовою,
х1
< 0 і х2
< 0, то
–2(а + 1) <
0 і 9а – 5 >
0.
З
другої нерівності знаходимо
а
> –1.
З
третьої нерівності знаходимо а > 5/9.
- Урок 1. Лінійне рівняння з одним невідомим і цілими вільними членами
- Урок 2. Лінійне рівняння з одним невідомим і дрібними вільними членами
- Урок 3. Застосування правил визначення невідомого доданка, зменшуваного і від'ємника для розв'язання задач
- Урок 4. Застосування правил визначення невідомого множника для розв'язання задач
- Урок 5. Розв'язування рівнянь, що зводяться до лінійних
- Урок 6. Розв'язування рівнянь із змінною в знаменнику
- Урок 7. Застосування правил визначення діленого і дільника для розв'язання задач
- Урок 8. Лінійне рівняння з двома невідомими
- Урок 9. Рішення лінійних рівнянь за допомогою графіків
- Урок 10. Лінійне рівняння з параметром
- Урок 11. Системи двох рівнянь першого степеня з двома невідомими
- Урок 12. Розв'язання систем рівнянь способом підстановки
- Урок 13. Розв'язання систем рівнянь способом алгебраїчного додавання
- Урок 14. Рішення лінійних систем рівнянь за допомогою графіків
- Урок 15. Розв'язування задач за допомогою систем лінійних рівнянь
- Урок 16. Системи трьох лінійних рівнянь з трьома невідомими
- Урок 17. Повне квадратне рівняння загального вигляду
- Урок 18. Зведене квадратне рівняння
- Урок 19. Теорема Вієта
- Урок 20. Неповні квадратні рівняння
- Урок 21. Розв'язання квадратного рівняння способом виділення квадрата двочлена
- Урок 22. Графічний спосіб розв'язування квадратних рівнянь
- Урок 23. Квадратний тричлен
- Урок 25. Дробові раціональні рівняння
- Урок 26. Задачі на складання квадратних рівнянь
- Урок 27. Рівняння кола
- Урок 28. Системи рівнянь другого степеня є двома невідомими
- Урок 29. Розв'язування задач за допомогою систем рівнянь другого степеня
- Урок 30. Перетин прямої з колом
- Урок 31. Рішення нелінійних систем рівнянь за допомогою графіків
- Урок 32. Системи рівнянь з параметрами
- Урок 33. Рівняння вищих степенів
- Урок 34. Розв'язання рівнянь способом заміни
- Урок 35. Розв'язання систем рівнянь способом заміни
- Урок 36. Задачі на знаходження чисел
- Урок 37. Задачі на знаходження цифр
- Урок 38. Рішення задач на змішування за допомогою рівнянь
- Урок 39. Рішення задач на змішування за допомогою систем рівнянь
- Урок 40. Ірраціональні рівняння


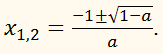


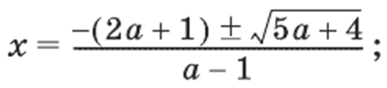





Комментариев нет:
Отправить комментарий