Щоб вирішити раціональне рівняння, потрібно:
– знайти спільний
знаменник усіх дробів;
- Замінити дане
рівняння цілим, помноживши обидві його частини на загальний знаменник;
- Вирішити отримане
ціле рівняння;
– виключити з його
коріння ті, які перетворюють на нуль спільний знаменник.
Один із способів розв’язування дробових рівнянь
полягає у заміні їх рівносильними рівняннями, в яких ліва частина – дріб, а
права – нуль.
– вирішити рівняння
А = 0.
– перевірити яке зі
знайденого коріння задовольняють умові
В ≠ 0.
– коріння, яке
задовольняє умову
В ≠ 0,
ПРИКЛАД:
РОЗВ’ЯЗАННЯ:
ПРИКЛАД:
Розв'яжіть рівняння:
РОЗВ'ЯЗАННЯ:х2 – 6х + 8
= 0.
знаходимо
х1 = 2, х2 = 4.
Залишилося
перевірити чи знайдене коріння звертають вираз 2х(2 – х) на нуль, тобто перевірити виконання умови
2х(2 – х) ≠ 0.
Помічаємо,
що 2
не задовольняє цю умову, а 4
задовольняє. Отже, х = 4 –
єдиний корінь рівняння.
ПРИКЛАД:
х ≠ –6, х ≠ 6.
ВІДПОВІДЬ: х = 4
ПРИКЛАД:
8х2 – 6х + 1 = 0,
х1 = 0,25, х2 = 0,5,
х ≠ –0,25, х ≠ 0,25.
ВІДПОВІДЬ: х = 0,5
ПРИКЛАД:
х1 = 1, х2 = 5,5,
х ≠ 0, х ≠ 2.
ВІДПОВІДЬ: х1 = 1, х2 = 5,5
ПРИКЛАД:
х1 = 1, х2 = –2,
х ≠ 2, х ≠ –2.
ВІДПОВІДЬ: х = 1
ПРИКЛАД:
х1 = 7, х2 = –2,
х ≠ 2, х ≠ –2,
ВІДПОВІДЬ: х = 7.
ПРИКЛАД:
х1 = 2, х2 = –4,
х ≠ 2, х ≠ 0.
ВІДПОВІДЬ: х = –4
ПРИКЛАД:
х1 = 1, х2 = –8,
х ≠ –8, х ≠ 8.
ВІДПОВІДЬ: х = 1
ПРИКЛАД:
х1 = 9, х2 = –5,
х ≠ –5, х ≠ 5.
ВІДПОВІДЬ: х = 9
ПРИКЛАД:
2х2 – 5х = 0
х1 = 0, х2 = 2,5,
х ≠ 0, х ≠ 1.
ВІДПОВІДЬ: х = 2,5
ПРИКЛАД:
х2
– 2х = 0,
х1 = 0, х2 = 2,
х ≠ 0, х ≠ –2.
ВІДПОВІДЬ: х = 2
ПРИКЛАД:
х2
+ 2х – 8 = 0,
х1 = –4, х2 = 2,
х ≠ 4, х ≠ –4.
ВІДПОВІДЬ: х = 2
ПРИКЛАД:
(х + 12)2 =
0,
х = –12,
х ≠ 0, х ≠ –4, х ≠ 4.
ВІДПОВІДЬ: х = –12
ПРИКЛАД:
х1 = 1, х2 = 2,
х ≠ 2, х ≠ –2.
- Урок 1. Лінійне рівняння з одним невідомим і цілими вільними членами
- Урок 2. Лінійне рівняння з одним невідомим і дрібними вільними членами
- Урок 3. Застосування правил визначення невідомого доданка, зменшуваного і від'ємника для розв'язання задач
- Урок 4. Застосування правил визначення невідомого множника для розв'язання задач
- Урок 5. Розв'язування рівнянь, що зводяться до лінійних
- Урок 6. Розв'язування рівнянь із змінною в знаменнику
- Урок 7. Застосування правил визначення діленого і дільника для розв'язання задач
- Урок 8. Лінійне рівняння з двома невідомими
- Урок 9. Рішення лінійних рівнянь за допомогою графіків
- Урок 10. Лінійне рівняння з параметром
- Урок 11. Системи двох рівнянь першого степеня з двома невідомими
- Урок 12. Розв'язання систем рівнянь способом підстановки
- Урок 13. Розв'язання систем рівнянь способом алгебраїчного додавання
- Урок 14. Рішення лінійних систем рівнянь за допомогою графіків
- Урок 15. Розв'язування задач за допомогою систем лінійних рівнянь
- Урок 16. Системи трьох лінійних рівнянь з трьома невідомими
- Урок 17. Повне квадратне рівняння загального вигляду
- Урок 18. Зведене квадратне рівняння
- Урок 19. Теорема Вієта
- Урок 20. Неповні квадратні рівняння
- Урок 21. Розв'язання квадратного рівняння способом виділення квадрата двочлена
- Урок 22. Графічний спосіб розв'язування квадратних рівнянь
- Урок 23. Квадратний тричлен
- Урок 24. Квадратні рівняння з параметрами
- Урок 26. Задачі на складання квадратних рівнянь
- Урок 27. Рівняння кола
- Урок 28. Системи рівнянь другого степеня є двома невідомими
- Урок 29. Розв'язування задач за допомогою систем рівнянь другого степеня
- Урок 30. Перетин прямої з колом
- Урок 31. Рішення нелінійних систем рівнянь за допомогою графіків
- Урок 32. Системи рівнянь з параметрами
- Урок 33. Рівняння вищих степенів
- Урок 34. Розв'язання рівнянь способом заміни
- Урок 35. Розв'язання систем рівнянь способом заміни
- Урок 36. Задачі на знаходження чисел
- Урок 37. Задачі на знаходження цифр
- Урок 38. Рішення задач на змішування за допомогою рівнянь
- Урок 39. Рішення задач на змішування за допомогою систем рівнянь
- Урок 40. Ірраціональні рівняння






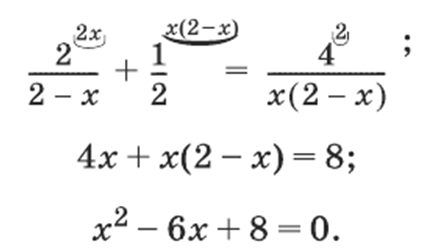


























Комментариев нет:
Отправить комментарий