Урок 18. Паралелограм

пятница, 28 ноября 2014 г.

Урок 18. Паралелограм

ВІДЕОУРОК

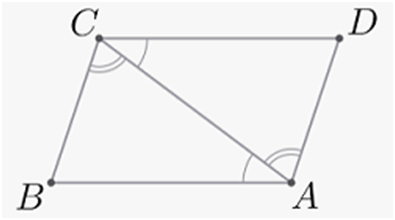
Паралелограм – чотирикутник, у якого протилежні сторони паралельні (тобто лежать на паралельних прямих).

Наприклад, АВСD – паралелограм, оскільки

АВ ॥ СD, BC ॥ AD.

Основні властивості паралелограма.

– протилежні сторони рівні;
– дві протилежні сторони паралельні;
– діагоналі діляться в точці перетину навпіл;
– протилежні кути рівні.
Наявність у чотирикутника однієї з цих властивостей або рівності або паралельності однієї пари протилежних сторін викликає, як наслідок, решту всіх властивостей.

Ознаки паралелограма.

– якщо дві сторони чотирикутника рівні та паралельні, то цей чотирикутник – паралелограм;

– якщо протилежні сторони чотирикутника попарно рівні, цей чотирикутник – паралелограм;

– якщо в чотирикутнику діагоналі перетинаються і в точці перетину діляться навпіл, то цей чотирикутник – паралелограм, а точка перетину діагоналей є його центром симетрії;

– сума кутів, прилеглих до однієї сторони, дорівнює 180°;
– діагональ ділить паралелограм на два рівних трикутника;
– сума квадратів діагоналей паралелограма дорівнює сумі квадратів його сторін.

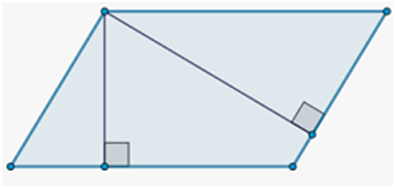
Висотою паралелограма називають перпендикуляр, опущений із будь-якої точки однієї сторони на протилежну сторону або її продовження.
– у паралелограмі кут між висотами дорівнює його гострому куту;
– бісектриси кутів, що прилягають до однієї сторони паралелограма, взаємно перпендикулярні;
– бісектриси двох протилежних кутів паралелограма паралельні.
ЗАДАЧА:

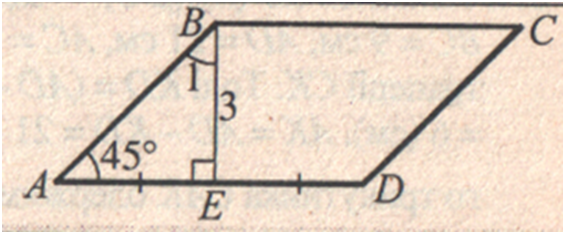
Один із кутів паралелограма дорівнює 45°. Його висота, опущена з вершини тупого кута, дорівнює 3 см і поділяє сторону паралелограма навпіл. Знайдіть цей бік паралелограма.

РОЗВ’ЯЗАННЯ:
∠ 1 = 90° – 45° = 45°,

АЕ = ВЕ = 3 (см).

АD = 2 ∙ АЕ = 2 ∙ 3 = 6 (см).

ЗАДАЧА:

Різниця двох кутів паралелограма дорівнює 20°. Знайдіть менший кут паралелограма.

РОЗВ’ЯЗАННЯ:

Позначимо менший кут – х,

тоді більший буде х + 20°.

Складемо рівняння:

х + х + 20° = 180°.

Вирішимо його:

2х = 160°, х = 80°.

ЗАДАЧА:

Сума двох кутів паралелограма дорівнює 168°. Знайти його кути.

РОЗВ’ЯЗАННЯ:

Двома заданими кутами можуть бути тільки протилежні кути паралелограма, бо сума кутів, які прилягають до однієї сторони дорівнює 180°. Отже, ці кути по

168° : 2 = 84°

(протилежні кути паралелограма рівні).

Тоді кожен із решти кутів по

180° – 84° = 96°.

ВІДПОВІДЬ: 84°, 96°.

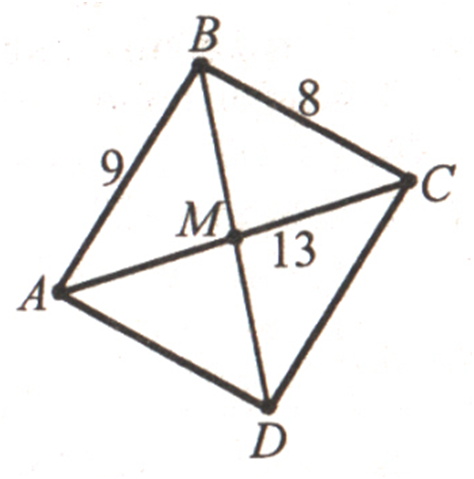
ЗАДАЧА:

Сторони трикутника дорівнюють 8 см, 9 см і 13 см. Знайдіть медіану трикутника, проведену до найбільшої сторони.

РОЗВ’ЯЗАННЯ:

Нехай АВС – заданий трикутник,
у якому

ВС = 8 см,

АВ = 9 см,

АС = 13 см,

ВМ – медіана, тому

МС = ¹/₂АС.

Відкладемо на продовженні медіани ВМ

МD = ВМ.

Отримаємо паралелограм АВСD (діагоналі чотирикутника точкою перетину діляться навпіл).

На підставі формули
запишемо:

ВD² + АС² = 2(АВ² + ВС²),

Знайдемо ВD:

ВD² + 13² = 2(9² + 8²),

ВD² = 121, ВD = 11.

Тепер знайдемо медіану ВМ:

ВМ = 0,5 ∙ ВD = 5,5 см.

ЗАДАЧА:

Сторони трикутника дорівнюють 6 см і 8 см. Медіана трикутника, проведена до третьої сторони, дорівнює √͞͞͞͞͞46 см. Знайдіть невідому сторону трикутника.

РОЗВ’ЯЗАННЯ:

Нехай АВС – заданий трикутник,
ВО – медіана,

ВС = 6 см,

АВ = 8 см,

ВО = √͞͞͞͞͞46 см.

На промені ВО побудуємо відрізок ОD так, що ОВ = ОD. У чотирикутнику АВСD діагоналі точкою перетину діляться навпіл, тому цей чотирикутник є паралелограмом. За властивістю діагоналей паралелограма отримаємо:

АС² + ВD² = 2АВ² + 2ВС²,

Найдём АС:

АС² + (2√͞͞͞͞͞46)² = 2(8² + 6²),

АС² = 200 – 184 = 16,

АС = 4 (см).

Завдання до уроку 18

Інші уроки:

Уроки математики и физики для школьников и родителей

пятница, 28 ноября 2014 г.