Перш ніж приступити до рішення прикладів і завдань, обов'язково ознайомтеся з теоретичною частиною уроку
Комбінації тіл (2)
1. Ребро
куба АВСDА1В1С1D1 дорівнює
6 см.
Знайти об'єм піраміди з основою ВDD1 і вершиною
С.
а) 32 см3;
б) 36 см3;
в) 38 см3;
г) 34 см3.
2. Сторона
основи правильної чотирикутної призми дорівнює
а,
а висота – Н.
Знайдіть об'єм циліндра, описаного навколо цієї призми.
4. У паралелепіпеді ABCDA1B1C1D1 проведено переріз через пряму BD і точку А1. Знайдіть об'єм паралелепіпеда, якщо об'єм піраміди A1ABD дорівнює F.
а) 4V;
б) 9V;
б) 9V;
в) 6V;
г) 2V.
г) 2V.
5. Точки M,
K
і P
– середини ребер
A1D1, D1C1 і DD1
куба ABCDA1B1C1D1 відповідно. Знайдіть об'єм піраміди
D1MKP,
якщо об'єм куба дорівнює V.
A1D1, D1C1 і DD1
куба ABCDA1B1C1D1 відповідно. Знайдіть об'єм піраміди
D1MKP,
якщо об'єм куба дорівнює V.
7. У циліндр вписано куб, об'єм якого дорівнює 8 см2. Знайти об'єм циліндра.
а) 3π см3;
б) 8π см3;
в) 4π
см3;
г) 2π
см3.
8.
Сторона основи правильної трикутної піраміди дорівнює 6 см,
а бічне ребро – 4 см.
Знайдіть об'єм конуса, описаного навколо цієї піраміди.
а) 8π
см3;
б) 12π см3;
в) 4π см3;
г) 6π см3.
9. Бічні
ребра піраміди дорівнює b,
а її основою є прямокутний трикутник з катетом
а і прилеглим до нього кутом β.
Знайдіть об'єм конуса, описаного навколо цієї піраміди.
10. Основою піраміди є ромб зі стороною 16 см і гострим кутом 60°.
Усі двогранні кути при основі піраміди дорівнюють 30°.
Знайдіть об'єм конуса, вписаного в дану піраміди.
а) 60π см3;
б) 62π см3;
в) 68π см3;
г) 64π см3.
11. Знайти відношення об'ємів кулі та вписаного в
неї куба.
12. Основою прямої призми є рівнобічна трапеція,
основи якої дорівнюють 8 і 2. Висота призми
дорівнює 10/π. Знайти об'єм циліндра,
вписаного в цю призму.
а) 40;
б) 36;
б) 36;





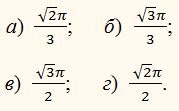
Комментариев нет:
Отправить комментарий