Урок 12. Об'єм циліндра

понедельник, 19 февраля 2018 г.

Урок 12. Об'єм циліндра

Якщо тіло просте, тобто допускає розбивку на кінцеве число трикутних пірамід, то його об'єм дорівнює сумі об'ємів цих пірамід. Для довільного тіла об'єм визначається в наступний спосіб.

Дане тіло має об'єм V, якщо існують прості тіла, що містять його, й прості тіла, що втримуються в ньому, з об'ємами, що як завгодно мало відрізняються від V.

Застосуємо це визначення до знаходження об'єму циліндра з радіусом основи R і висотою H.

При виводі формули для площі кругу були побудовані такі два n-кутника (один – що містить коло, інший – що втримується в колі), що їхні площі при необмеженому збільшенні n необмежено наближалися до площ кругу. Побудуємо такі багатокутники для кола в основі циліндра. Нехай Р – багатокутник, що містить коло, Р' – багатокутник, що втримується в колі.

Побудуємо дві прямі призми з основами Р и Р' и висотою Н, яка дорівнює висоті циліндра. Перша призма містить циліндр, а друга призма втримується в циліндрі. Так як при необмеженому збільшенні n площі основ призм необмежено наближаються до площі основи циліндра S, то їхні об'єми необмежено наближаються до SH.

За величину об'єму циліндра приймають границю, до якої наближаються об'єми правильних вписаних в циліндр (або описаних навколо нього) призм при необмеженому збільшенні числа їх бічних граней. Зауважимо, що коли число граней правильної призми необмежено збільшується, то довжина основи кожної з них обов'язково буде наближатися до нуля.

Об'єм циліндра дорівнює добутку площі його основи на висоту:

ЗАДАЧА:

Знайти діагональ осьового перерізу циліндра, якщо об'єм циліндра дорівнює 240π дм³, а бічна поверхня 120π дм².

РОЗВ'ЯЗАННЯ:

За умовою

V_цил = 240π дм³,
S_ABCD = 120π дм².

Знайти АС.

Позначимо AD = R і AD = H, одержимо систему рівнянь

πR²H = 240π,

2πRH = 120π,

звідки

R = 4 дм, а
Н = 15 дм.

Далі з прямокутного трикутника АDС знаходимо

ВІДПОВІДЬ: 17 дм.

ЗАДАЧА:

Два однакові рівносторонні циліндри

(DM = MN = 2R = a)

розміщені так, що вісь одного з них є твірною другого. Знайти об'єм їх спільної частини AEDFF₁BE₁C.

РОЗВ'ЯЗАННЯ:

Легко показати, що об'єм спільної частини циліндрів

V = AB × S_AEDF.

Площа спільної частини основ AEDF дорівнює сумі площ двох однакових сегментів.

Оскільки EF ⊥ AD і ділить радіус основи циліндра AD пополам, то EF – сторона правильного вписаного в основу ∆ EMF, тобто

EF = R√͞͞͞͞͞3 і дуга
EDF має 120°.

Тоді

S_сегм
FAE =
S_сект_DFAE – S_∆_DFE.

Враховуючи, що за умовою

R = AD = ^a/₂,

маємо

В цьому випадку площа спільної частини основ циліндрів

і шуканий об'єм

ВІДПОВІДЬ:

ЗАДАЧА:

У відро циліндричної форми вміщується 10 л води. Іграшкове відро має розміри у 10 разів менше. Скільки літрів води вміщується у іграшкове відро ?

РОЗВ’ЯЗАННЯ:

Літр – одиниця вимірювання об’єму (1 л = 1 дм³).

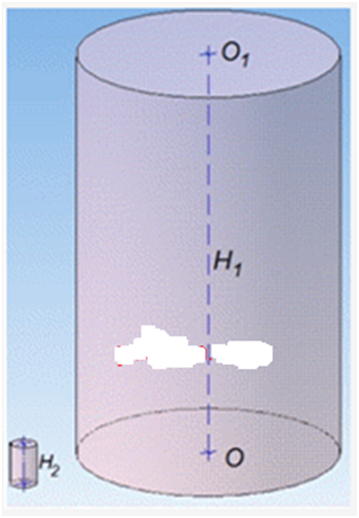
Маємо велике відро є об’ємом V₁ = 10 л, висотою Н₁, та іграшкове відро об’ємом V₂, висотою Н₂.

Оскільки за умовою задачі розміри іграшкового відра в 10 разів менше, то

Н₁= 10Н₂

(тобто розміри великого відра в 10 разів більше за іграшкове).
Всі (прямі) циліндри подібні, а у подібних тіл, за властивістю, відношення об’ємів дорівнює відношенню їх відповідних лінійних розмірів, взятих у кубі, тобто:

Отже, V₂ = 0,01 л – об’єм іграшкового відра, тобто кількість води, яку вміщує іграшкове відро.

ВІДПОВІДЬ: 0,01 л

ЗАДАЧА:

У циліндричний посуд, в якому знаходиться 10 літрів води, опущена деталь. При цьому рівень рідини у посудині піднявся у 2,4 рази. Чому дорівнює обсяг деталі ?

РОЗВ’ЯЗАННЯ:

Об'єм витісненої рідини – і є обсяг деталі. Об'єм витісненої рідини дорівнює 1,4 вихідного об'єму (якщо припустити, що початкова висота стовпчика рідини дорівнює Н, то нова висота стовпчика – 2,4Н, тобто різниця – 1,4Н), тому обсяг деталі дорівнює 1,4 від вихідного об'єму, тобто