Правильна трикутна призма.
Правильна шестикутна призма.
ЗАДАЧА:
ЗАДАЧА:
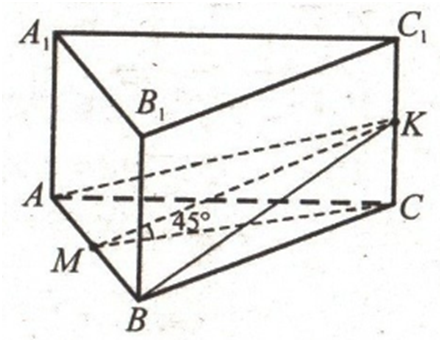
Через
сторону нижньої основи і середину протилежного бічного ребра правильної
трикутної призми проведено площину, яка утворює з площиною основи кут 45°. Площа утвореного перерізу
дорівнює 16√͞͞͞͞͞6 см2. Знайдіть об’єм призми.
РОЗВ'ЯЗАННЯ:
S∆КАВ = 16√͞͞͞͞͞6 см2.
Проведемо КМ
⊥
АВ. За теоремою про три
перпендикуляри СМ ⊥
АВ. Тому ∠ КМС
– лінійний кут двогранного кута, утвореного площиною КАВ і площиною основи. За умовою, ∠ КМС = 45°. У трикутнику
КМС (∠ С = 90°),
∠ К = ∠ М = 45°.
Тому МС = КС. Трикутник САВ є проекцією трикутника КАВ,
тому
S∆ABC = S∆КАВ
∙ cos ∠ KMC =
=
16√͞͞͞͞͞6 ∙
cos 45°
=
= 1/2
(16√͞͞͞͞͞6 ∙
√͞͞͞͞͞2
) = 16√͞͞͞͞͞3 (см2).
Оскільки
трикутник АВС – рівносторонній, то
S∆ABC =
1/4
AB2√͞͞͞͞͞3.
1/4
AB2√͞͞͞͞͞3 = 16√͞͞͞͞͞3, AB2
=
64,
AB = 8 см, MB = 4 см.
З ∆ CМB (∠ M = 90°):
CM = МB tg 60° = 4√͞͞͞͞͞3 (см),
KC = CM = 4√͞͞͞͞͞3 см,
CC1 = 2KC = 8√͞͞͞͞͞3
см.
Vпр. = Sосн.∙ H = S∆АВС
∙ C1C =
= 16√͞͞͞͞͞3 ∙ 8√͞͞͞͞͞3 =
384 (см3).
ВІДПОВІДЬ: 384
см3
ЗАДАЧА:
Через
сторону нижньої основи і протилежну вершину верхньої основи правильної
трикутної призми проведено площину, яка утворює з площиною основи кут 60°.
Площа утвореного перерізу дорівнює 8√͞͞͞͞͞3 см2. Знайдіть об’єм призми.
РОЗВ'ЯЗАННЯ:
S∆АВС = S∆АВС1 ∙ cos ∠ С1МС.
S∆АВС = 8√͞͞͞͞͞3 ∙ cos 60° =
= 1/2 ∙ 8√͞͞͞͞͞3 =
4√͞͞͞͞͞3 (см2).
S∆АВС = 1/4 ∙ AB2√͞͞͞͞͞3
.
1/4 ∙ AB2√͞͞͞͞͞3
= 4√͞͞͞͞͞3,
AB2 = 16, AB
= 4 (см).
S∆АВС = 1/2 AB ∙ MC,
4√͞͞͞͞͞3 = 1/2 ∙ 4 ∙ MC,
MC = 2√͞͞͞͞͞3 (см).
З ∆ C1CM (∠ C = 90°):
C1C = МC tg ∠ C1MC =
= 2√͞͞͞͞͞3 tg 60° = 2√͞͞͞͞͞3 ∙√͞͞͞͞͞3
= 6 (см),
Vпр. = Sосн.∙ H =
= 4√͞͞͞͞͞3 ∙
6 = 24√͞͞͞͞͞3 (см3).
ВІДПОВІДЬ: 24√͞͞͞͞͞3 см3
ЗАДАЧА:
У
прямокутній трикутній призмі всі бічні грані є квадратами зі стороною 10√͞͞͞͞͞3. Знайдіть об’єм призми.
РОЗВ'ЯЗАННЯ:
Площа рівностороннього трикутника знаходимо за такою формулою:Vпризми = S ∙ Н,
Vпризми = 75√͞͞͞͞͞3 ∙ 10√͞͞͞͞͞3 = 2250.
- Урок 1. Одиниці вимірювання об'ємові
- Урок 2. Об'єм прямий призми
- Урок 3. Об'єм похилої призми
- Урок 5. Об'єм прямого паралелепіпеда
- Урок 6. Об'єм похилого паралелепіпеда
- Урок 7. Об’єм прямокутного паралелепіпеда
- Урок 8. Об’єм куба
- Урок 9. Об’єм піраміди
- Урок 10. Об’єм правильної піраміди
- Урок 11. Об’єм зрізаної піраміди
- Урок 12. Об’єм циліндра
- Урок 13. Об’єм конуса
- Урок 14. Об’єм зрізаного конуса
- Урок 15. Об’єм кули та її частин
- Урок 16. Тіла обертання
- Урок 17. Комбінації тіл (2)
- Урок 18. Правильні багатогранники
- Урок 19. Об’єм подібних тіл









Комментариев нет:
Отправить комментарий