Якщо наповнити посудину вологим піском, а потім
перевернути її і зняти, то утвориться фігура такого самого об’єму, як і
посудина.
Для обчислення обсягів користуються результатами
отриманими італійським математиком Бонавентура Кавальєрі, учнем Галілея, який
сформулював так званий «принцип Кавальєрі» для обчислення обсягів усіх фігур.
Пояснимо зміст цього принципу.
Уявімо собі фізичну модель, дуже схожу на
чотирикутну піраміду, складену з тонких (наприклад, картонних) квадратиків
послідовно спадних розмірів.
Сформулюємо цей принцип у більш спільній ситуації.
Якщо всі горизонтальні поперечні перерізи двох наших
фігур, що знаходяться на тому самому рівні, мають одну й ту саму площу, то дві
наші фігури мають один і той самий обсяг.
Принцип Кавальєрі ми сприймаємо як основну
властивість виміру обсягів.
Нехай нам дано дві фігури F1 та F2 та площину α. Якщо кожна площина,
паралельна площині α,
перетинаючи одну фігуру, перетинає також і іншу, причому утворені при цьому
перерізи даних фігур мають рівні площі, дані фігури мають один і той же обсяг.
Поняття
об’єма
фігур.
Об’єм – це величина, яка задовольняє наступним властивостям:
– кожна фігура має
певний об’єм, виражений позитивним числом;
– рівні фігури мають рівні об’єми.
Одиницею виміру об'єму є об'єм куба з довжиною ребра а, де а – одиниця
виміру довжини. Цей обсяг позначається а3.
Об'єм куба зі стороною а дорівнює
а3.
Vкуба = а3,
де а
– ребро куба.
Якщо одиницю довжини приймається 1 мм,
то одиницею обсягу є 1 мм3 (кубічний міліметр).
Якщо одиницю довжини приймається 1 см,
то одиницею обсягу є 1 см3 (кубічний сантиметр).
Часто, особливо у
повсякденній діяльності, використовуються невеликі обсяги рідин. Їх буває
непросто уявляти. На відміну, наприклад, від літра. Кубічний дециметр
називається літром (л). Відразу бачиться літрова банка, яку всі знають.
Літр зазвичай використовується для вимірювання обсягів рідин – молока, гасу та
ін. Літровий кухоль вміщує 1
дм3 рідини. Маса 1 літра води становить 1000
г, тобто 1 кг. Вимірюють рідини ще й у мілілітрах.
1 л = 1000 мл.
Перед приготуванням
якоїсь страви часто необхідно розрахувати кількість продуктів. Якщо вони
вимірюються у грамах чи кілограмах, то зробити це порівняно легко.
Але як бути, якщо за
рецептом потрібна вода, олія, сироп ? Все те, що є рідиною. На допомогу прийде
вже існуючи переведення мілілітрів у літри. Таким чином, достатньо розділити
ту кількість мілілітрів, яка вказана рецептурі, на тисячу. І вийде потрібне
значення літрів. Наприклад, 100
мл ділимо на 1000 і отримуємо 0,1 л.
500 і 1000
мл відповідно –
це 0,5
та
1 л.
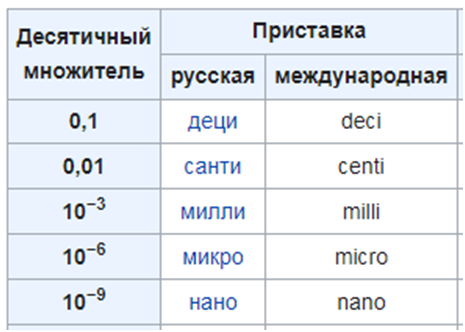
Міжнародна система
одиниць багата на різні приставки, що допомагають позначати обсяг, довжину і
вагу. Так, тисячні частки стандартних одиниць вимірювальної рідини позначаються
приставкою милі.
При необхідності
переведення одиниць виміру, досить згадати значення приставки – тисяча. Це
допоможе вирішувати питання, що виникають, з мірою рідини.
Завдання до уроку 1
- Урок 2. Об’єм прямий призми
- Урок 3. Об’єм похилої призми
- Урок 4. Об’єм правильної призми
- Урок 5. Об’єм прямого паралелепіпеда
- Урок 6. Об’єм похилого паралелепіпеда
- Урок 7. Об’єм прямокутного паралелепіпеда
- Урок 8. Об’єм куба
- Урок 9. Об’єм піраміди
- Урок 10. Об’єм правильної піраміди
- Урок 11. Об’єм зрізаної піраміди
- Урок 12. Об’єм циліндра
- Урок 13. Об’єм конуса
- Урок 14. Об’єм зрізаного конуса
- Урок 15. Об’єм кули та її частин
- Урок 16. Тіла обертання
- Урок 17. Комбінації тіл (2)
- Урок 18. Правильні багатогранники
- Урок 19. Об’єм подібних тіл





Комментариев нет:
Отправить комментарий