Урок 23. Ромб

понедельник, 1 декабря 2014 г.

Урок 23. Ромб

ВІДЕОУРОК
Ромб – це паралелограм, у якого всі сторони рівні.

ПРИКЛАД:

ABCD – ромб,

AB = BC = CD = AD.

Оскільки ромб – це паралелограм, то він має всі властивості паралелограма, а також властивості, характерні лише для нього.

Властивості ромба.

– діагоналі ромба взаємно перпендикулярні;

– діагоналі ромба є бісектрисами його кутів.

Ознаки ромба.

– паралелограм, діагоналі якого взаємно перпендикулярні є ромбом;

– паралелограм, діагоналі якого є бісектрисами його кутів, є ромбом.

ЗАДАЧА:

Кут між висотою ромба, проведеною з вершини тупого кута, і його стороною дорівнює 25°. Чому дорівнює менший з кутів ромба ?

РОЗВ’ЯЗАННЯ:

Из ∆ АКВ (∠ К = 90°):

∠ А = 90° – 25° = 65°.

ЗАДАЧА:

У ромбі АВСD кут АВD дорівнює 75°. Чому дорівнює кут ВСD ?

РОЗВ’ЯЗАННЯ:

∠ ABC = 2∠ ABD =

= 2 ∙ 75° = 150°,

∠ BCD = 180° – 150° = 30°.

ЗАДАЧА:

Один з кутів ромба дорівнює 60°. Знайдіть меншу діагональ ромба, якщо його сторона дорівнює 15 см.

РОЗВ’ЯЗАННЯ:

Накреслимо креслення.

∆ АВD – рівнобедрений з кутом 60° при вершині, тому – ∆ АВD рівносторонній,

ВD = АD = 15 см.

ЗАДАЧА:

У ромбі АВСD кут А дорівнює 120°. Укажіть вид трикутника АВС ?

РОЗВ’ЯЗАННЯ:

АС – бісектриса кута А, тому

∠ САВ = 120° : 2 = 60°,

АВ = ВС,

тому трикутник АВС – рівнобедрений. .

Так як,

∠ АСВ = ∠ САВ = 60°,

Отже, ∠ АСВ = ∠ САВ = 60°,

тому трикутник АВС – рівносторонній.

ЗАДАЧА:

Сторона ромба дорівнює 5 см, а діагональ – 8 см. Знайдіть іншу діагональ ромба.

РОЗВ’ЯЗАННЯ:

З ∆ АОВ:

АС = 2АО = 2 ∙ 3 = 6 (см).

ЗАДАЧА:

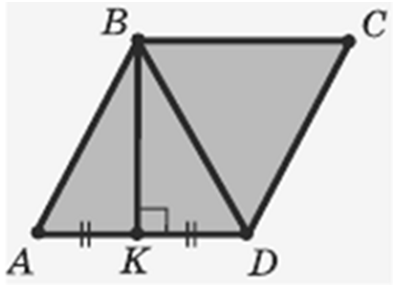
Знайдіть кути ромба, якщо основа перпендикуляра, опущеного з вершини тупого кута, ділить сторону ромба навпіл.

РОЗВ’ЯЗАННЯ:

З умови завдання маємо:

АВСD – ромб.

АВ = ВС = СD = DА.
ВК ⊥ АD, АК = DК.

Потрібно знайти кути ромба.

Проведемо діагональ ромба ВD.

∆ АВD – рівнобедрений з основою ВD,

∆ АВD – рівнобедрений з основою АD,

значить ∆ АВD – рівносторонній.

∠ А = 60°,

∠ А = ∠ С = 60°,

∠ В = ∠ D = 120°.

ЗАДАЧА:

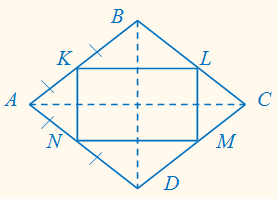
Яку фігуру одержимо, якщо послідовно сполучимо середини сторін ромба ?

РОЗВ'ЯЗАННЯ:

Сторони одержаного чотирикутника є середніми лініями трикутників, що їх утворюють діагоналі ромба з його сторонами, а тому вони паралельні до діагоналей. Діагоналі ромба взаємно перпендикулярні, отже, і суміжні сторони одержаного чотирикутника теж; тому побудований чотирикутник є прямокутником.

ЗАДАЧА:

Знайти невідомий кут ромба.

РОЗВ'ЯЗАННЯ:

∠ АСК = 40° (протилежні кути ромба рівні).

∆ АСК – рівнобедрений (сторони ромба рівні).

Тому кути при основі АК рівні. За властивістю кутів ромба маємо

х + х + 40° = 180°.

Тоді х = 70°.

ВІДПОВІДЬ: 70°

Завдання до уроку 23

Інші уроки:

Уроки математики и физики для школьников и родителей

понедельник, 1 декабря 2014 г.