Урок 25. Трапеція

вторник, 2 декабря 2014 г.

Урок 25. Трапеція

ВІДЕОУРОК
Трапеція – чотирикутник, дві сторони якої паралельні, а дві інші не паралельні.

Основи трапеції – її паралельні сторони.

Бічні сторони трапеції – її непаралельні сторони.

ABCD – трапеція,

BC ∥ AD, AB ∦ CD.

Прямокутна трапеція – трапеція, у якої один з кутів прямої.

Середня лінія трапеції – відрізок, що сполучає середини її бічних сторін.

Середня лінія трапеції паралельна підставам і дорівнює їх напівсумі.

ПРИКЛАД:

ABCD – трапеція,

KM – середня лінія,

KM ∥ AD, BC ∥ KM,

KM = ¹/₂ (AD + BC).

У кожній трапеції сума двох кутів, що прилягають до бічної сторони, дорівнює 180°.

ЗАДАЧА:

Основа трапеції дорівнює 10 см, а її середня лінія – 7 см. Знайдіть іншу основу трапеції.

РОЗВ'ЯЗАННЯ:

Нехай х см – інша основа трапеції, тоді середня лінія дорівнює:

ЗАДАЧА:

Основи трапеції відносяться як 3 : 7, а її середня лінія дорівнює 80 см. Знайдіть меншу основу трапеції.

РОЗВ'ЯЗАННЯ:

Нехай менша основа 3х см, тоді більша – 7х см.
5х = 80, х = 16 (см).

Тоді менша основа:

3х = 3 ∙ 16 = 48 (см).

ЗАДАЧА:

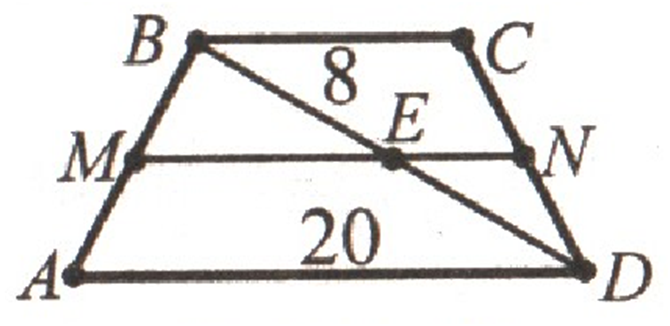
Знайдіть відрізки, на які ділить середню лінію діагональ трапеції, основи якої дорівнюють 8 см і 20 см.

РОЗВ'ЯЗАННЯ:

Накреслимо креслення.
МЕ – середня лінія ∆ АВD,

МЕ = ¹/₂ АD = ¹/₂∙ 20 = 10 (см).

EN – середня лінія ∆ ВDC,

EN = ¹/₂ DC = ¹/₂∙ 8 = 4 (см).

ВІДПОВІДЬ: 10 (см), 4 (см)

ЗАДАЧА:

Гострий кут прямокутної трапеції на 40° менший від тупого кута. Знайдіть гострий кут.

РОЗВ'ЯЗАННЯ:

Нехай х – гострий кут,

тоді х + 40° – тупий.

х + х + 40° = 180°,

х = 70°.

ЗАДАЧА:

Продовження бічних сторін АВ і СD трапеції АВСD перетинаються в точці Е. Знайдіть відрізок ЕD, якщо СD = 8 см,

ВС : АD = 3 : 5.

РОЗВ'ЯЗАННЯ:

Накреслимо креслення.

3х + 24 = 5х,

2х = 24, х = 12 (см).

ЕD = 8 + 12 = 20 (см).

ЗАДАЧА:

Основи трапеції дорівнюють 4 і 10. Знайдіть більший з відрізків, на які ділить середню лінію цієї трапеції одна з його діагоналей.

РОЗВ'ЯЗАННЯ:

Нехай MN – середня лінія трапеції, S – точка перетину діагоналі АС і середній лінії МN. По властивості середньої лінії трапеції МN ∥ AD. Оскільки N – середина CD, то по теоремі Фалеса S – середина АС. Значить, SN – середня лінія трикутника АСD за визначенням. Тоді по властивості середньої лінії трикутника

Аналогічно MS = 2.

SN – більший з відрізків середньої лінії.

ВІДПОВІДЬ: 5

ЗАДАЧА:

Основі трапеції дорівнюють 12 і 60. Знайдіть відрізок, що сполучає середини діагоналей трапеції

РОЗВ'ЯЗАННЯ:

Середня лінія трапеції містить точки – середини діагоналей.

NM – частина середньої лінії.

Потому

ВІДПОВІДЬ: 24

ЗАДАЧА:

Більша основа трапеції дорівнює 20 см, а відстань між серединами її діагоналей – 6 см. Яка довжина меншої основи трапеції ?

РОЗВ'ЯЗАННЯ:

Накреслимо креслення.
Нехай АВСD – задана трапеція (ВС ∥ АD),

АD = 20 см.

Проведемо середню лінію трапеції МN. Тоді МN перетне діагоналі АС і ВD у точках К і F (оскільки МК ∥ ВС і точка М є серединою АВ, FN ∥ ВС і точка N є серединою СD).

Точки К і F є середини діагоналей трапеції і КF = 6 см. Відрізок КF є середньою лінією трикутника АСD, тому

КN = 20 : 2 = 10 (см).

Отже,

КF + FN = 10,

6 + FN = 10,

FN = 4 (см).

У трикутнику ВDС відрізок FN – середня лінія. Тоді

ВС = 2FN = 8 (см).

ВІДПОВІДЬ: 8 см

ЗАДАЧА:

Діагоналі трапеції АВСD (ВС ǀǀ АD) перетинаються в точці О,

АО : ОС = 7 : 3,

АС = 40 см.

Знайдіть довжину відрізка АО.

РОЗВ'ЯЗАННЯ:

Накреслимо креслення.
7х + 3х = 40,

10х = 40, х = 4,

АО = 7 ∙ 4 = 28 (см).

ЗАДАЧА:

Відрізок АВ – діаметр кола, АВ = 24 см. Точка А віддалена від дотичної до цього кола на 4 см. Знайдіть відстань від точки В до цієї дотичної.

РОЗВ'ЯЗАННЯ:

Накреслимо креслення.
R = 24 : 2 = 12 см,

АDQВ – трапеція (АD ∥ ВQ),

ОК – середня лінія. Отже:

QВ = 20 (см).

Завдання до уроку 25

Інші уроки:

Уроки математики и физики для школьников и родителей

вторник, 2 декабря 2014 г.