Урок 4. Окружность

среда, 17 декабря 2014 г.

Урок 4. Окружность

ВИДЕОУРОК

Длина окружности.

Возьмём круглый стакан, поставим его на лист бумаги и обведём его карандашом.

На бумаге получится окружность.

Если мы возьмём циркуль и установим неподвижно одну его ножку (с острым концом) в точку, а другую (с карандашом) будем вращать по плоскости вокруг неподвижной точки, не меняя раствора циркуля, то карандаш опишет замкнутую кривую линию, все точки которой будут находиться на одинаковом расстоянии от указанной неподвижной точки. Мы получим кривую линию, которая называется окружностью.

Окружность – геометрическая фигура, которая состоит из всех точек, расположенных на заданном расстоянии от данной точки – центра окружности.

Внутренняя область окружности называется кругом. Граница круга его окружность.

Другими словами, окружность – это контур круга (то, что мы рисуем циркулем). Круг – та часть листа бумаги, которая остаётся внутри.

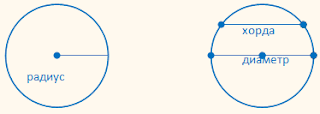
Точка, оставленная циркулем острым концом, называется центром окружности. Расстояние от центра до любой точки окружности называется её радиусом. Из построения следует, что все радиусы одной окружности равны между собой. Отрезок прямой линии, соединяющий две любые точки окружности и проходящий через её центр, называется диаметром. Диаметр равен двум радиусам. Следовательно, все диаметры одной окружности равны между собой. Диаметр окружности обычно обозначают буквой d или D. Диаметр равен двум радиусам:

d = 2r, D = 2R.

Если обвязать стакан ниткою, а потом разровнять её, то длина нитки будет приближённо равна длине нарисованной окружности.

Чем больше диаметр окружности, тем больше его длина. Для всех окружностей отношение длины окружности к его диаметру будет одним и тем же числом. Это число обозначают греческою буквою π.

Если обозначить длину окружности буквою С, а длину диаметра буквою d, то длину окружности находят по следующей формуле:

C = πd.

Так как диаметр окружности вдвое больше чем его радиус, то длина окружности с радиуса r равна 2πr. Получим другую формулу для длины окружности:

C = 2πr,

То есть, чтобы найти длину окружности, надо его диаметр умножить на π, или два радиуса умножить на π.

Расчёты показали, что с точностью до десятичных π ≈ 3,1415… . Если значение числа π округлить до сотых, то получим значение 3,14. Примерно такую точность даёт значение π ≈ ²²/₇.

ЗАДАЧА:

Определить радиус окружности, если она длиннее своего диаметра на 107 см.

РЕШЕНИЕ:

Обозначим длину окружности как С, а диаметр как D. Таким образом

С – D = 107.

Длина окружности равна

C = πD,

поэтому
Откуда радиус окружности
Дуга окружности.

Дуга окружности – каждая из двух частей окружности, на которые окружность делится двумя точками.
∪ АВ – дуга окружности.

Полуокружность – дуга, концы которой являются концами диаметра окружности.

∪ СТ – полуокружность, так как отрезок СТ – диаметр.

Дуги окружности измеряются в градусах.

Отрезок прямой линии, соединяющий две любые точки окружности и не проходящий через её центр, называется хордой окружности.

Диаметр окружности, который проходит через середину хорды, перпендикулярен к ней. Диаметр, перпендикулярный к хорде, делит её и дугу, которую она стягивает, пополам. Справедливо и обратное утверждение: если диаметр окружности проходит через середину хорды, которая не является диаметром, или через середину дуги, на которую она опирается, то этот диаметр перпендикулярен к этой хорде. Равные дуги стягиваются равными хордами, а равные хорды опираются на равные дуги. Дуги, которые лежат между параллельными хордами, равны.

Взаимное расположение прямой и окружности.

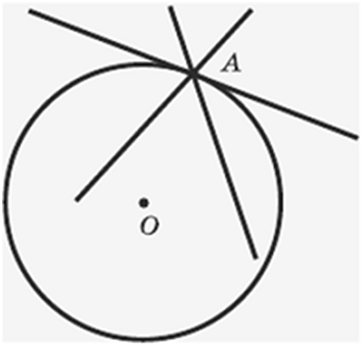
Известны три случая взаимного размещения прямой и окружности, если эта прямая и окружность лежат в одной плоскости:

– прямая и окружность не имеют общих точек;

– прямая и окружность имеют одну общую точку;

– прямая и окружность имеют две общие точки.

Перечислим условия, определяющие все возможные случаи взаимного расположения прямой и окружности, в зависимости от расстояния между центром окружности и прямой.

– если расстояние от центра окружности до некоторой прямой больше радиуса, то эта прямая не имеет с окружностью общих точек, при этом окружность лежит по одну сторону от прямой;
– если расстояние от центра окружности до прямой равно радиусу, то окружность имеет с прямой единственную общую точку, то есть прямая касается окружности и в этом случае окружность лежит по одну сторону от прямой.
Прямая, которая имеет с окружностью одну общую точку, называется касательной к окружности. При этом данная точка окружности называется точкой касания. Касательная к окружности не имеет с ней других общих точек, кроме точки касания.

Справедливо следующее:

– касательная к окружности перпендикулярна к радиусу, проведённого в точку касания;

– если прямая перпендикулярна радиусу окружности и проходит через его конец, лежащий на окружности, то она является касательной к этой окружности;

– если из данной точки провести две касательных к окружности, то отрезки касательных, которые соединяют данную точку с точками касания, равны.

Все точки касательной, кроме точки касания, лежат вне данной окружности. Действительно, если предположить, что на касательной имеется хотя бы одна точка, лежащая внутри окружности, то прямая должна пересекать окружность в двух точках, поэтому она не может быть касательной.

Прямая и окружность могут иметь только одну общую точку, но через эту точку может проходить бесконечное множество прямых, не лежащих с окружностью в одной плоскости.

– если расстояние от центра окружности до некоторой прямой меньше радиуса, то эта прямая имеет с окружностью две общих точки, то есть прямая пересекает окружность и разбивает окружность на две части, прямую, которая пересекает окружность в двух точках, называют секущей;
Если прямая проходит через точку, внутреннюю относительно окружности, то она является секущей, то есть пересекает окружность в двух точках.

ЗАДАЧА:

Сколько общих точек имеет прямая и окружность, диаметр которой равен 8 см, если прямая расположена на расстоянии 5 см от центра окружности ?

РЕШЕНИЕ:

Если диаметр окружности равен 8 см, тогда радиус будет равен 4 см. Расстояние от центра окружности до прямой – 5 см, значит, окружность и прямая не пересекаются.
Расположение окружностей.

Две окружности могут быть расположены так:

– окружности не имеют общих точек.

Они находятся: или одна вне второй окружности, в этом случае расстояние между центрами будет больше чем сумма радиусов, или одна в середине второй, в этом случае расстояние между центрами будет меньше чем разность радиусов.

– окружности имеют общую точку.

Окружности, которые имеют одну общую точку, называются касательными. Общую точку называют точкой касания. Говорят, что две окружности, которые имеют общую точку, в которой касаются, имеют и общую касательную.

Касание окружностей называется внутренним, если центры окружностей находятся по одну сторону от общей касательной.
Касание окружностей называется внешним, если центры окружностей находятся по разные стороны от их общей касательной.
ЗАДАЧА:

Две окружности диаметром 4 см и 8 см касаются внешним образом. Чему равно расстояние между центрами окружностей ?

РЕШЕНИЕ:

Радиусы окружностей ОА и О₁А перпендикулярны их общей касательной, проходящей через точка А.
Поэтому

ОО₁ = ОА + О₁А = 6 см.

ЗАДАЧА:

Две окружности касаются внешне. Найти длину общей внешней касательной, если радиусы окружностей равны 16 см и 25 см.

РЕШЕНИЕ:

O₁D₁ ⊥ OD₁, O₂D₂ ⊥ OD₁.

Обозначим точку Е на O₂D₂, так что O₁E D₂D₁– прямоугольник, тогда

O₂E = R₂ – R₁ = 9 (см),

O₁O₂ = R₂ + R₁ = 41 (см).

∆ O₁O₂E: (∠ E = 90°),

ОТВЕТ: 40 см

ЗАДАЧА:

Какое взаимное расположение двух окружностей с диаметрами 10 см и 20 см, если расстояние между их центрами равно 15 см ?

РЕШЕНИЕ:
Окружности пересекаются в одной точке.

– окружности имеют две общие точки.

В этом случае расстояние между центрами будет меньше чем сумма их радиусов или больше чем их разность.

Прямую, которая проходит через центры двух окружностей, называют линией центров. Две окружности находящиеся в одной плоскости и имеющие общий центр, называются концентрическими окружностями.

Окружность – геометрическое место точек, равноудалённых от данной точки. Круг радиуса r – геометрическое место точек, расстояние от которых до данной точки не превышает r.

Если хорды АВ и СD окружности пересекаются в точке S, то

АS × ВS = СS × DS.

Если из точки Р до окружности проведено две секущие, которые пересекают окружность соответственно в точках А, В и С, D, то

АР × ВР = СР × DР.

ПРИМЕР:

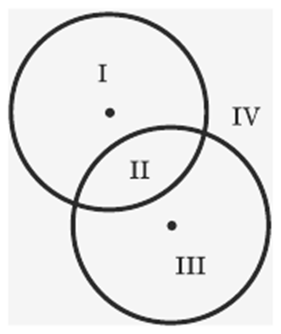
На какое наибольшее число различных частей, не имеющих общих точек, кроме своих границ, могут разбивать плоскость:

а) две окружности;

б) три окружности ?

РЕШЕНИЕ:

Изобразим на рисунке соответствующие условию случаи взаимного расположения фигур. Запишем ответ:

а) четыре части,
б) восемь частей.

Задания к уроку 4

Другие уроки:

Уроки математики и физики для школьников и родителей

среда, 17 декабря 2014 г.